Problems of the CSP Model

Problems of the CSP model

In the CSP model all the knowledge about the problem must be known before the resolution process begins. In the vision system this means that the feature extracting process must terminate before the resolution process starts. If all we wanted was just 'find out if there is a rectangle in a given figure', then we would waste a lot of computation time to extract segments which will never be used. This inefficiency is ought to the intrinsic seriality of the two main processes: the feature extraction process and the recognition process. Also, there is no way in such an architecture for the CSP system to guide the vision system; the information flow is unidirectional, from the low-level system to the high level system.

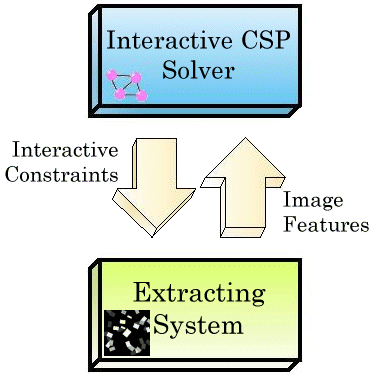
Interactive Architecture A more efficient architecture would execute both the processes in parallel, and would allow bi-directional communication between the processes. The architecture we propose is made up of two systems communicating:

A high-level system, which uses a constraint model to recognize shapes. This system guides the feature extraction by means of constraints.
A low-level system, which extracts image features consistent with the constraints communicated by the high-level system.

In such an architecture, the high level system must be able to cope with incomplete information, i.e. it does not know all of the values in the variable domains. Values must be acquired during the computation process, requesting them to the low-level system by means of constraints.

The ICSP Model

To obtain this, we define an Interactive CSP (ICSP) model which has to:

Cope with incomplete domain definition. Variable domains can be partially defined, i.e. some values belonging to the domain can be already known and others have to be acquired.
Requesting information when needed, thus interacting with the low-level system and performing knowledge acquisition on demand.
Guide feature extraction by means of constraints. The CSP solver must generate new constraints on the base of already acquired knowledge.
Incrementally process new information without restarting a constraint propagation process from scratch each time new information is available.

On the basis of this requirements, we define the ICSP model as follows:

Definition 1. An interactive CSP (ICSP) is defined on a finite set of variables {X₁, X₂, ..., X_n} each ranging on a partially defined domain {D₁, D₂, ... , D_n} where each D_i = [Def_i È UnDef_i]. Def_i represents the defined part, while UnDef_i is a variable itself representing information which is not yet available. Both Def_i and UnDef_i can possibly be empty (if both are empty an inconsistency arises). Also, for each i, Def_i Ç UnDef_i = Æ. A constraint among variables defines a possibly partially defined subset of the cartesian product of variable domains.

A solution of an ICSP is, as in the CSP case, an assignment of values to variables which satisfies all the constraints. The constraint propagation is, instead, quite different. When propagating a constraint c(X_i,X_j), we have to propagate four kinds of constraints: c(Def_i,Def_j), c(Def_i,UnDef_j), c(UnDef_i,Def_j) and c(UnDef_i,UnDef_j) (We refer, with an abuse of notation, to domains instead of variables; however, the meaning is straightforward). The constraint propagation between the defined parts of domains is like in usual CSP propagation; while propagating constraints on the undefined parts of domains may imply acquisition.

Implementation issues

Given the general definition, we still have some freedom degrees, which let us implement different search strategies. Also, the capabilities of the low-level system may influence the choices we make.
Probably, we will do value acquisition using other values; e.g. we will ask "Find all the numbers lower than 5" rather than "Find couples of values such that the first is less than the second", because the second query would make the low-level system perform hard tasks. Since the low-level system is usually the slowest, we want the high-level system to do the hard work. This means that propagation among only undefined parts, i.e. c(UnDef_i,UnDef_j), will be suspended until more information is available.
Other freedom degrees we have to consider are:

which of the constraints we consider will perform acquisition and which will not;
how many values we should acquire;
when to perform acquisition.

We will answer to this questions in the next paragraphs.

Which constraints are to be considered interactive

We may decide that not every kind of constraint can cause the system to perform acquisition; in such an instance we will distinguish between interactive and non interactive constraints. In the vision example, the low-level system is able to find features in a specified subpart of the image, so only constraints expressing locality should be considered as interactive constraints. For example, if we decide that acquisition must be performed by means of the parallel(s₁,UnDef_j) constraint, the low-level system will be forced to scan the entire image to find the segments with the same inclination of segment s₁; on the other hand, if we decide to acquire with the touch(s₁,UnDef_j) constraint, then the low-level system will search other segments only near the end points of segment s₁. It's worth noting that using constraints expressing locality to perform acquisition, we obtain a system capable of selective attention, i.e. a system which is able to set its focus of attention only in semantically significant parts of the image. This is an important issue in visual search, because an image contains enormous quantities of data and the recognizing system has limited processing capabilities.
In other systems, we can select as interactive candidates the constraints which are very tight, i.e. only few domain values satisfy them. This choice will yield only few acquisitions for each propagation step (See also the Experimental Results section).

How many values we should acquire

We can decide to acquire one single consistent value or all the consistent values. In some problems, acquiring all the consistent values is a single basic task; e.g. in the vision system, acquiring all the segments which start from one point has the same complexity as acquiring one single segment. In other systems, the acquisition is performed sequentially, so it's suitable to postpone it until it's strictly necessary.

When to perform acquisition

We can decide to perform acquisition only if one of the variables is bound (it has been assigned a value), or even if it has some values in its domain. This will influence the number of consistency inference we perform during search. As in classical CSP solving, after assigning a value to a variable, we can decide to check consistency with the variables still unbound (as in Forward checking [vHent89] ) or something more (e.g. enforcing arc-consistency [vHent89] ).

Specializing the generic ICSP model to different search strategies

This choices to be made are strictly bound each others, and we can use the freedom degrees to specialize the generic ICSP propagation to match corresponding CSP solving techniques. We used them in order to implement different search strategies, that we call Interactive Forward Checking (IFC) and Interactive Minimal Forward Checking (IMFC).

Interactive Forward Checking

In classic CSP solving, the Forward Checking strategy interleaves a labeling step and a propagation step [vHent89]. In the labeling step a variable X_i is istantiated to a value v in its domain. In the propagation step all the values in unbound variable domains inconsistent with the assignment X_i/v are removed (so the domain will contain only values consistent with all the constraints).
In the interactive version of Forward Checking, both the steps must consider that variable domains can be partially defined, or even completely undefined (i.e. no values in the domain are known - all have to be acquired). In the labeling step, first we look for values in the defined part of domains; if there are none (or if those values have already been tested and they led to failure), we try values in the undefined part of the domain. Those values have to be acquired, by means of interactive constraints (if there are any), or by means of unguided acquisition; then they are assigned to the variable. For the first variable, guided acquisition can be performed only if there are interactive unary constraints imposed on it; for the other variables there will be at least one constraint on it (if the constraint graph is connected), so we can perform guided acquisition.
In the propagating move, the propagation of the constraint w.r.t. the defined part of domains (say constraint c(v,Def_j) ) is like in ordinary CSP propagation, as asserted before. This means that all the values belonging to Def_j which are not consistent with value v are removed. In the propagation of constraint c(v,UnDef_j), acquisition is performed; in this case all the values consistent with v will be acquired. The resulting domain will be completely specified (i.e. the undefined part will be empty) and it will contain the same elements as after ordinary Forward Checking propagation. It's worth noting that each variable domain, during computation, is either fully known (i.e. the Unknown part is empty) or fully unknown (i.e. the Known part is empty).

Interactive Minimal Forward Checking

The Minimal Forward Checking algorithm [DM94] is based on the idea to maintain only one consistent value in each future-connected domain, postponing constraint checks until necessary. This implies that a value in future domains must be checked even with respect to the past connected variables. When propagating a constraint c(v,X_j), if the first value in domain(Xj) is consistent w.r.t. value v, the propagation of the constraint terminates (i.e. we consider propagation of another constraint). If the first value is not consistent, then it is removed and another candidate must be found; this element must be checked with respect to all the past-connected variables, because it was not checked when propagating the former constraints. This way a lot of constraint checks is avoided, because many domain values are not checked for consistency.
In the interactive version of Minimal Forward Checking, only one consistent value is kept in the Known part of domains, while other values are represented in the Unknown part. This means that values which are not checked for consistency aren't even extracted, thus avoiding many extractions. When propagating a constraint c(v,Xj), if the first value in domain(Xj) is consistent w.r.t. value v, the propagation is over; if it is not, the value is removed and another value must be acquired. The newly acquired value must be checked with all the past assignments. In other words, when we check a value in the defined part of the domain, we act as in ordinary MFC; then, if the domain is fully unknown, we perform acquisition.
The labeling step is similar as in the IFC case: if there is a unary interactive constraint imposed on a variable, then it can be used to acquire the first value; otherwise the computation can start by acquiring a value with unguided acquisition. For the other variables, a value is a value is always present in the Defined part of domain, and it can be assigned to the variable. During backtracking, the value is removed from the domain and another acquisition is performed by means of the interactive past constraints.

Previous Main Page Next