Funzione fprintf

La funzione fprintf stampa con formattazione controllata:

L’interfaccia della funzione è:

function fprintf(FORMAT, E1, E2, ...)

• FORMAT è una stringa da stampare
• E1, E2 sono espressioni (e.g. nomi di variabile)
• FORMAT può contenere dei “segnaposto”, con il carattere %
  • E.g. %f è un segnaposto per un valore reale
  • E.g. %d è un segnaposto per un valore intero
• Il primo segnaposto è sostituito con il valore di E1
• Il secondo segnaposto è sostituito con il valore di E2, etc.

Funzione fprintf

Vediamo un esempio:

A = 10.5;
B = 2;
fprintf('A = %f, B = %f, A*B = %f\n', A, B, A*B)

Stampa: A = 10.500000, B = 2.000000, A*B = 21.000000

• “\n” è un carattere speciale e serve ad andare a capo

I segnaposto cono configurabili

Ci interessa un caso solo: “%.Nf” stampa un reale con N valori decimali

• E.g. %.3f stampa con 3 cifre decimali
• E.g. %.1f stampa con 1 cifra decimale

Ciclo while

Il ciclo for non è sempre adeguato ad implementare iterazioni:

• E.g. quando non è desiderabile limitare il numero di iterazioni a priori

Per questi casi, Matlab fornisce il ciclo while

La sintassi è:

while <espressione> % vera o falsa
  <corpo>
end

• Il corpo viene ripetuto…
• …Fintanto che <espressione> denota true (o \(\neq 0\))

Funzione Zeta di Riemann

Consideriamo la funzione Zeta di Riemann ed il nostro vecchio codice:

\[\zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s}\]

z = 0;                      % val. della somma
old_z = -Inf;               % vecchio z
for n = 1:10000               % 1e5 = iterazioni massime
  z = z + 1 ./ n.^s;
  if abs(z - old_z) < 1e-6  % 1e-6 è la tolleranza
    break                   % Interrompe il ciclo
  end
  old_z = z;                % rimpiazzo il vecchio z
end

• Cosa succede se 10000 iterazioni non bastano a convergere?

Funzione Zeta di Riemann

Consideriamo la funzione Zeta di Riemann ed il nostro vecchio codice:

\[\zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s}\]

z = 0;                      % val. della somma
n = 1;
old_z = -Inf;               % vecchio z
while abs(z - old_z) > 1e-6 % 1e-6 è la tolleranza
  old_z = z;                % memorizzo il vecchio z
  z = z + 1 ./ n.^s;
  n = n + 1;                % incremento n
end

• Fintanto che \(|z - old_z| > 1e-6\), il ciclo prosegue

Funzione Zeta di Riemann

Consideriamo la funzione Zeta di Riemann ed il nostro vecchio codice:

\[\zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s}\]

z = 0;                      % val. della somma
n = 1;
old_z = -Inf;               % vecchio z
while abs(z - old_z) > 1e-6 % 1e-6 è la tolleranza
  old_z = z;                % memorizzo il vecchio z
  z = z + 1 ./ n.^s;
  n = n + 1;                % incremento n
end

• Dobbiamo però gestire l’indice n esplicitamente

Cicli Infiniti

Il ciclo while non fornisce garanzie di terminazione

Per esempio:

n = 1;
s = 0;
while n < 10
  s = s + n;
end

• Questo ciclo non termina
• Perché n non viene incrementato!

Se vi capita, niente panico: basta premere [CTRL+C]

• Capita più spesso di quanto ci si possa aspettare :-)

Equilibrio di Sistemi Tempo-Discreti

Consideriamo un sistema dinamico tempo-discreto

In generale è definito da una equazione del tipo:

\[x^{(t+1)} = f(x^{(t)})\]

Per questo tipo di sistemi, abbiamo imparato a:

• Osservare l’andamento dello stato del tempo
• Identificare il tipo di comportamento (convergente, periodico…)
• Per i sistemi convergenti, individuare uno stato di equilibrio…
• …Simulando sufficientemente a lungo e misurando lo stato finale

Gli stati di equilibrio, però, si possono determinare a priori!

Determinazione degli Stati di Equilibrio

Uno stato è di equilibrio se viene “trasformato in se stesso”

Formalmente, uno stato di equilibrio \(x\) deve soddisfare:

\[x = f(x)\]

• Manca l’indice di tempo, perché lo stato a sx e dx è lo stesso

Se risolviamo l’equazione, determiniamo gli stati di equilibrio

• In generale \(x\) è un vettore, quindi \(x = f(x)\) è un sistema di equazioni
• Se \(f(x)\) è lineare, possiamo usare la forma matriciale:

\[A x = b\]

E possiamo risolverlo con i metodi visti in analisi numerica

Un Esempio: Pagerank

Per l’algoritmo pagerank, visto la scorsa lezione

L’equazione fondamentale è data da:

\[x^{(t+1)} = p \underbrace{\frac{1}{n}}_{\text{vettore}} + (1-p) P x^{(t)}\]

Uguagliando \(x^{(t+1)}\) e \(x^{(t)}\) otteniamo:

\[I x = p \frac{1}{n} - (1-p) P x\]

\[\underbrace{(I - (1-p) P)}_{A} x = \underbrace{p \frac{1}{n}}_{b}\]

• \(A\) è quadrata per costruzione (deriva da una transizione di stato)
• Quindi, in casi normali, la soluzione è data da \(x = A^{-1} b\)

Un Esempio: Pagerank

Supponendo di disporre delle variabili:

• p, per la probabilità di stancarsi
• P, per la matrice delle probabilità di click
• n, per il numero delle pagine

Possiamo prima costruire la matrice \(A\) e la colonna \(b\):

A = (eye(n) - (1-p)*P) % eye e' la matrice identita'
b = (ones(n,1) * p/n) % ones(n,1) per avere una colonna

E quindi possiamo calcolare la soluzione con una divisione sinistra:

xeq = A \ b

Equilibrio di Sistemi Tempo-Discreti Non Lineari

L’approccio è valido anche per sistemi dinamici non lineari

Uno stato, per essere di equilibrio, deve soddisfare:

\[x = f(x)\]

• I.e. la relazione che abbiamo già visto!
• …Che corrisponderà però \(x\) ad un sistema di equazioni non lineari

Ce ne occuperemo più avanti nel corso

Simulare o Non Simulare?

Quando risolvere un sistema di equazioni e quando simulare?

Simuliamo se:

• Ci interessa il comportamento nel tempo
• Il sistema non ha uno stato di equilibrio (e.g. periodico, caotico)
• Vogliamo determinare (empiricamente) la stabilità dell’equilibrio
• …

Risolviamo le equazioni se:

• Non ci interessa il comportamento nel tempo
• Non ci interessa la stabilità (basta uno stato di equilibrio)
• Se dobbiamo calcolare lo stato di equilibrio con alta precisione
• …

Stati di Equilibrio Multipli

Un sistema dinamico tempo discreto lineare:

• Ha sempre un solo stato di equilibrio…
• …A meno che la matrice dei coefficienti non sia singolare

Per esempio, per le previsioni del tempo (scorsa lezione) avevamo:

\[\begin{align} x^{(t+1)} = P x^{(t)} \quad\text{ con }\quad P = \left(\begin{array}{cc} 0.9 & 0.5 \\ 0.1 & 0.5 \\ \end{array}\right) \end{align}\]

Da cui si ottiene il sistema:

\[(I - P) x = 0 \quad\text{ con }\quad \begin{aligned} (I-P) = \left(\begin{array}{cc} 0.1 & -0.5 \\ -0.1 & 0.5 \\ \end{array}\right) \end{aligned}\]

• Possiamo usare la funzione det per calcolare il determinante:

det(eye(2) - A) % -1.1102e-17 (sarebbe 0)

Stati di Equilibrio Multipli

Cosa vuol dire in pratica?

• Un sistema sotto-determinato ha infinite soluzioni…
• …Quindi ci sono infiniti stati di equilibrio

Per esempio, supponiamo di avere due vasi comunicanti

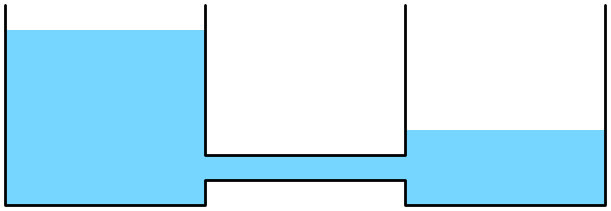
• Il livello finale dipende da quanta acqua c’è nel sistema!
• In questo specifico caso, lo stato raggiunto dipende dallo stato iniziale…
• …Altre volte, ci sono dei vincoli sottointesi

Esercizio: Previsioni del Tempo

Nel caso delle previsioni del tempo:

Il tempo è bello o brutto, quindi la somma delle probabilità deve essere 1

• Partiamo dalle equazioni originali per l’equilibrio:

\[\begin{align} 0.1 x_g - 0.5 x_b = 0\\ -0.1 x_g + 0.5 x_b = 0 \end{align}\]

• Una delle due equazioni può essere rimossa…
• …Ma possiamo anche aggiungere \(x_g + x_b = 1\)

\[\begin{align} 0.1 x_g - 0.5 x_b = 0\\ x_g + x_b = 1 \end{align}\]

Nel file es_weather.m:

• Determinate lo stato di equilibrio risolvendo il sistema lineare
• Verificate che coincide con lo stato raggiunto dalla simulazione

Equilibrio di Sistemi Tempo-Continui Lineari

Una stanza è ventilata mediante una sola apertura:

• Sia \(T_o\) temperatura esterna, \(T_a\) quella dell’aria interna
• Sia \(T_w\) la temperatura dei muri

Il flusso di calore tra l’esterno e l’aria è dato da:

\[i_1 = \frac{1}{R_1}(T_o - T_a)\]

• Dove \(R_1\) è la resistenza termica dell’apertura

Il flusso di calore tra l’aria e i muri è dato da:

\[i_2 = \frac{1}{R_2}(T_a - T_w)\]

• Dove \(R_1\) è la resistenza termica tra l’aria ed i muri

Equilibrio di Sistemi Tempo-Continui Lineari

Per quanto riguarda le temperature:

• La temperatura dell’esterno e dei muri si suppone costante
• La temperatura dell’aria varia con i flussi di calore

In particolare vale la relazione:

\[\frac{d T_a}{d t} = \frac{1}{C_a} (i_1 - i_2)\]

• Il flusso di calore \(i_1\) va dall’esterno all’aria, mentre \(i_2\) va dall’aria ai muri
• \(C_a\) è la capacità termica dell’aria

Per completezza, ricordiamo che:

\[\begin{align} i_1 &= \frac{1}{R_1}(T_o - T_a) & i_2 &= \frac{1}{R_2}(T_a - T_w) \end{align}\]

Equilibrio di Sistemi Tempo-Continui Lineari

Questo è un primo esempio di sistema dinamico tempo-continuo

I sistemi dinamici tempo continui sono descritti mediante equazioni differenziali

• Tipicamente, queste sono nella forma:

\[\dot{x} = f(x)\]

• Non sappiamo risolvere le equazioni differenziali…
• …Vedremo come farlo verso la fine del corso

Possiamo però già osservare che:

• Per definizione all’equilibrio lo stato non varia…
• …Il che vuol dire che le derivate si annullano

Il generale, un sistema tempo continuo all’equilibrio deve soddisfare:

\[f(x) = 0\]

Equilibrio di Sistemi Tempo-Continui Lineari

Nel nostro esempio abbiamo:

\[\begin{align} \frac{d T_a}{d t} &= \frac{1}{C_a} (i_1 - i_2) & i_1 &= \frac{1}{R_1}(T_o - T_a) & i_2 = \frac{1}{R_2}(T_a - T_w) \end{align}\]

Quindi, all’equilibrio avremo:

\[\begin{align} 0 &= \frac{1}{C_a} (i_1 - i_2) \\ i_1 &= \frac{1}{R_1}(T_o - T_a) \\ i_2 &= \frac{1}{R_2}(T_a - T_w) \end{align}\]

• È un sistema di equazioni lineari in \(i_1, i_2, T_a\)

E questo sappiamo come risolverlo!

Esercizio: Temperatura di una Stanza

Partiamo dal sistema originale:

\[\begin{align} 0 &= \frac{1}{C_a} (i_1 - i_2) \\ i_1 &= \frac{1}{R_1}(T_o - T_a) \\ i_2 &= \frac{1}{R_2}(T_a - T_w) \end{align}\]

• Le variabili sono \(i_1, i_2, T_a\)…
• …Ci conviene portarle a sx del segno =

Esercizio: Temperatura di una Stanza

Partiamo dal sistema originale:

\[\begin{align} \frac{1}{C_a} (i_1 - i_2) &=0 \\ i_1 + \frac{1}{R_1} T_a &= \frac{1}{R_1}T_o \\ i_2 - \frac{1}{R_2}T_a &= \frac{1}{R_2} T_w \end{align}\]

• Ora possiamo portarlo in forma matriciale

Esercizio: Temperatura di una Stanza

Partiamo dal sistema originale:

\[\left(\begin{array}{ccc} \frac{1}{C_a} & - \frac{1}{C_a} & \\ 1 & & \frac{1}{R_1} \\ & 1 & -\frac{1}{R_2} \\ \end{array}\right) \left(\begin{array}{c} T_a \\ i_1 \\ i_2 \end{array}\right) = \left(\begin{array}{c} 0 \\ \frac{1}{R_1}T_o \\ -\frac{1}{R_2}T_w \end{array}\right)\]

• Ogni riga è la trascrizione di una equazione
• Ogni colonna della matrice è associata ad una variabile…
• …Perché viene moltiplicata per tale variabile

Se chiamiamo la matrice \(A\) ed il termine noto \(b\), abbiamo:

\[A x = b\]

• Possiamo risolverlo con una divisione sinistra!

Esercizio: Temperatura di una Stanza

Partite dal file es_temperature.m nello start-kit

• Impostate la matrice dei coefficienti
• Impostate la colonna dei termini noti
• Risolvete il sistema per \(T_o = 17, T_w = 21\) e per \(T_o = 28, T_w = 21\)
• Stampate il valore di \(T_a\) all’equilibrio

Problemi di Interpolazione (Vincolata)

Si vuole progettare una arcata a ridosso di una parete verticale

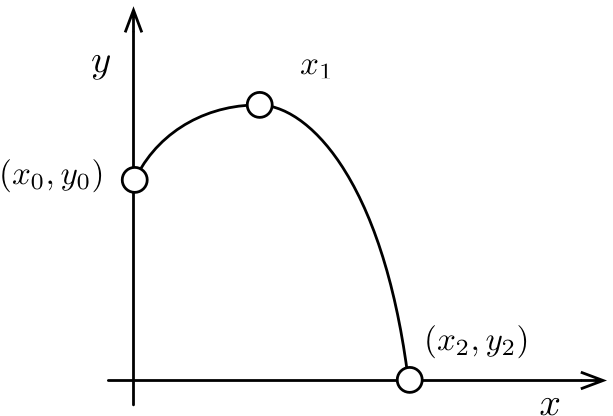
La curva che descrive l’arcata:

• Deve essere ancorata ad un punto noto \((x_0, y_0)\) sulla parete
• Deve essere ancorata ad un punto noto \((x_2, y_2)\) a terra
• Deve raggiungere l’altezza massima per \(x = x_1\) (con \(x_1\) noto)

Problemi di Interpolazione (Vincolata)

Un approccio: trattiamo la curva come una funzione \(f(x)\)

In questo modo possiamo tradurre le condizioni in equazioni:

• Deve essere ancorata ad un punto noto \((x_0, y_0)\) sulla parete

\[f(x_0) = y_0\]

• Deve essere ancorata ad un punto noto \((x_2, y_2)\) a terra

\[f(x_2) = y_2\]

• Deve raggiungere l’altezza massima per \(x = x_1\) (con \(x_1\) noto)

\[f'(x_1) = y_1\]

Così come sono ci dicono ben poco…

Tracciamento di Curve

Ci serve una assunzione sulla classe della funzione \(f(x)\)

Per esempio: \(f(x)\) è polinomiale. Formalmente:

\[f(x) = \sum_{i=0}^n \alpha_i x^i\]

Le nostre condizioni allora diventano:

\[\begin{align} & \text{passaggio per } (x_0, y_0) && \sum_{i=0}^n \alpha_i x_0^i = y_0 \\ & \text{passaggio per } (x_1, y_1) && \sum_{i=0}^n \alpha_i x_2^i = y_2 \\ & \text{annullamento di } f'(x_1) && \sum_{i=1}^n i \alpha_i x_1^{i-1} = 0 \end{align}\]

Tracciamento di Curve

Ci siamo quasi! Guardiamole meglio:

\[\begin{align} & \text{passaggio per } (x_0, y_0) && \sum_{i=0}^n \alpha_i x_0^i = y_0 \\ & \text{passaggio per } (x_1, y_1) && \sum_{i=0}^n \alpha_i x_2^i = y_2 \\ & \text{annullamento di } f'(x_1) && \sum_{i=1}^n i \alpha_i x_1^{i-1} = 0 \end{align}\]

Quali sono le incognite?

• Sono i parametri della funzione \(\alpha_i\) e non le \(x\)!

Che grado di polinomio ci serve?

• Tre condizioni \(\Rightarrow\) tre variabili, i.e. \(\alpha_0, \alpha_1, \alpha_2\) \(\Rightarrow\) secondo grado

Tracciamento di Curve

In questo modo otteniamo il sistema:

\[\begin{align} \alpha_2 x_0^2 + \alpha_1 x_0 + \alpha_0 &= y_0 \\ \alpha_2 x_2^2 + \alpha_1 x_2 + \alpha_0 &= y_2 \\ 2 \alpha_2 x_1 + \alpha_1 &= 0 \end{align}\]

• Che è lineare nelle incognite \(\alpha_2, \alpha_1, \alpha_0\)

La tecnica vista è un metodo generale per progettare curve:

• Si ipotizza una struttura per la curva da costruire (e.g. polinomio)
• Si traducono i vincoli del problema in equazioni
• Si risolvono le equazioni per determinare i parametri
  • Per ora consideriamo il caso in cui le equazioni sono lineari

Esercizio: Progettazione di un’Arcata

Consideriamo il sistema per il problema di progettazione dell’arcata:

\[\begin{align} \alpha_2 x_0^2 + \alpha_1 x_0 + \alpha_0 &= y_0 \\ \alpha_2 x_2^2 + \alpha_1 x_2 + \alpha_0 &= y_2 \\ 2 \alpha_2 x_1 + \alpha_1 &= 0 \end{align}\]

A partire dal file es_arc.m nello start-kit:

• Si determinino i coefficienti della curva risolvendo il sistema
• Si disegni la forma dell’arcata
• Si stampi a video il valore dell’altezza massima

Esercizio: Letto di un Fiume

Si vuole progettare lo scavo per il letto di un fiume

La sezione dello scavo deve presentarsi come segue:

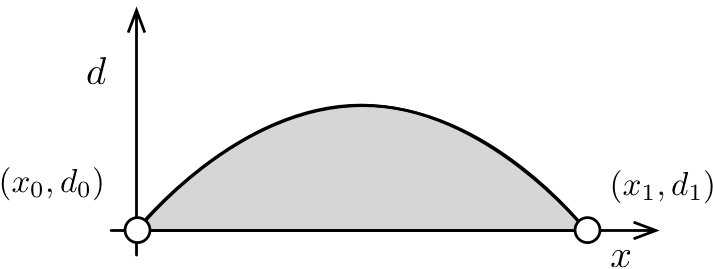
• La coordinata \(x\) rappresenta una posizione orizzontale
• La coordinata \(d\) rappresenta la profondità dello scavo
  • Per questa ragione la sezione si presenta “al contrario”

Esercizio: Letto di un Fiume

Si vuole progettare lo scavo per il letto di un fiume

• La sezione deve essere descritta da una curva parabolica
• Deve passare per i punti noti \((x_0, y_0)\) e \((x_1, y_1)\)
• L’area della sezione determina la portata massima…
• …E deve essere pari ad un valore prestabilito \(s_1\)

Se \(f(x)\) è la funzione che descrive la curva, l’area della sezione è:

\[S = \int_{\underbrace{x_0}_{= 0}}^{x_1} f(x) \, dx\]

A partire dal file es_riverbed.m nello start-kit:

• Si determinino i coefficienti della curva
• Si disegni la forma della sezione

Esercizio: Controllo di Accelerazione

Si vuole controllare l’accelerazione di un carrello automatico

Il profilo di velocità in accelerazione deve presentarsi come segue:

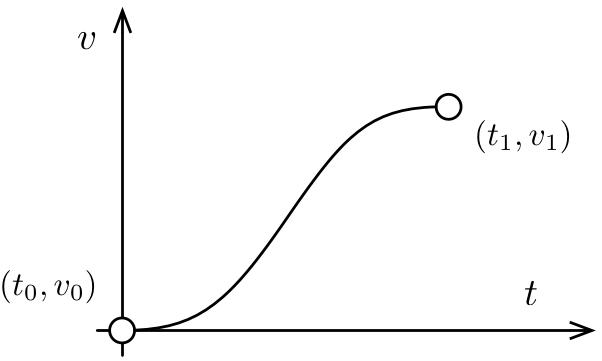
• La coordinata \(t\) rappresenta il tempo
• La coordinata \(v\) rappresenta la velocità

Curve di questo tipo si utilizzano nelle centraline di controllo di auto e moto

Esercizio: Controllo di Accelerazione

Si vuole controllare l’accelerazione di un carrello automatico

• Il profilo deve seguire un andamento polinomiale
  • Il grado del polinomio è da determinare
  • Servirà un coefficiente per ogni condizione specificata
• La velocità iniziale e finale ed il tempo di accelerazione \(t_1\) sono noti
• Perché le variazioni non siano troppo brusca…
• …Si richiede che la derivata della velocità in \(t_0\) e \(t_1\) sia nulla

A partire dal file es_acceleration.m nello start-kit:

• Si determinino i coefficienti della curva
• Si disegni il profilo della velocità in accelerazione

Esercizio: Controllo di Frenata

Si vuole controllare l’arresto di un carrello automatico

Il profilo di velocità in frenata deve presentarsi come segue:

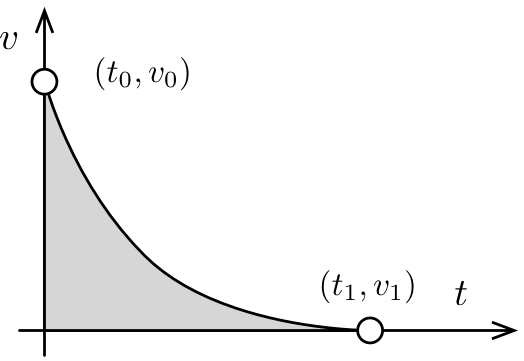
• La coordinata \(t\) rappresenta il tempo
• La coordinata \(v\) rappresenta la velocità

Possiamo usare la curva per programmare una centralina di controllo

Esercizio: Controllo di Frenata

Si vuole controllare l’arresto di un carrello automatico

• Il profilo è dato da un polinomio, di grado da determinare
• La velocità iniziale e finale ed il tempo di frenata \(t_1\) sono noti
• Si richiede che la derivata della velocità in \(t_1\) sia nulla
• Lo spazio di frenata \(S\) deve essere pari ad un valore \(s_1\), dove:

\[S = \int_{\underbrace{t_0}_{=0}}^{t_1} f(t) \, dt\]

A partire dal file es_brake.m nello start-kit:

• Si determinino i coefficienti della curva
• Si disegni il profilo della velocità in frenata

Esercizio: Progettazione di un Telaio

Si vuole progettare un telaio per una bicicletta

La forma del telaio deve apparire come segue:

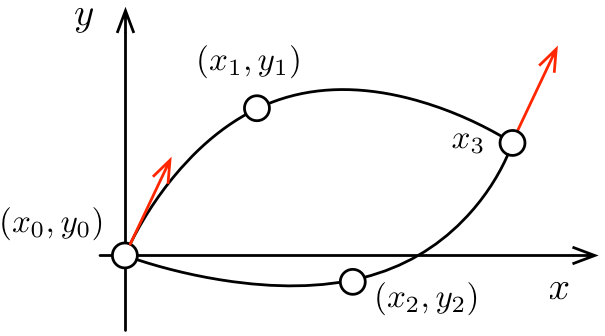
Esercizio: Progettazione di un Telaio

Si vuole progettare un telaio per una bicicletta

• La forma del telaio è descritta da due curve paraboliche \(f_1\) ed \(f_2\)
• Le due curve originano in un punto comune \((x_0 y_0)\)
• La curva \(f_1\) deve passare per l’ancoraggio della sella in \((x_1, y_1)\)
• La curva \(f_2\) deve passare per l’ancoraggio dei pedali in \((x_2, y_2)\)
• Le due curve devono congiungersi in un punto \((x_3, y_3)\)…
• …Di cui è nota solo la coordinata \(x_3\)
• Le derivate di \(f_1\) in \(x_0\) ed \(f_2\) in \(x_3\) devono essere uguali

Esercizio: Progettazione di un Telaio

A partire dal file es_frame.m nello start-kit:

• Si determinino i coefficienti delle due curve
• Si disegni il profilo del telaio

Attenzione:

Ci sono due condizioni che coinvolgono entrambe le curve:

• Le due curve devono congiungersi in un punto \((x_3, ???)\)
• Le derivate di \(f_1\) in \(x_0\) ed \(f_2\) in \(x_3\) devono essere uguali

Non possono essere formulate separatamente!

• Occorrerà definire un’unico sistema di equazioni…
• …in cui compaiono sia \(f_1(x)\) che \(f_2(x)\)