Approssimazione di una Derivata

Consideriamo questo problema di derivazione numerica:

• Data una generica funzione \(f: \mathbb{R} \mapsto \mathbb{R}\)…
• …Possiamo calcolare \(f'(x)\)?

Approssimazione di una Derivata

Consideriamo questo problema di derivazione numerica:

• Data una generica funzione \(f: \mathbb{R} \mapsto \mathbb{R}\)…
• …Possiamo calcolare \(f'(x)\)?

Consideriamo due casi:

• Se \(x\) non è noto, non è facile capire cosa fare
• Ma se \(x\) è noto (i.e. \(x = 1\)), allora sappiamo che:

\[f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h}\]

A questo punto:

• Se consideriamo un \(h\) molto piccolo…
• …Dovremmo ottenere una approssimazione decente

Scelta di \(h\)

Idealmente:

• Il valore di \(h\) dovrebbe essere più piccolo possibile…
• …Quindi \(h = \varepsilon\), con $= $ il più piccolo numero rappresentabile

In realtà non è una grande idea:

• Tende a generare errori di cancellazione
• Molto meglio usare questo secondo approccio:

\[h = \left\{\begin{aligned} & \sqrt{\varepsilon} x & \text{ if } |x| > tol \\ & \sqrt{\varepsilon} & \text{ altrimenti} \end{aligned} \right.\]

• Dove \(tol\) è un valore di tolleranza

Proviamo a Codificarlo

Proviamo ad abbozzare una implementazione:

function df = derive(...)
  if abs(x) > 1e-6 % Scelta di h
    h = sqrt(eps) * x;
  else
    h = sqrt(eps)
  end
  df = 1/h * (f(x+h) - f(x)) % Calcolo della derivata
else

• Un parametro è x (il punto per cui calcolare la derivata)…

Proviamo a Codificarlo

Proviamo ad abbozzare una implementazione:

function df = derive(...)
  if abs(x) > 1e-6 % Scelta di h
    h = sqrt(eps) * x;
  else
    h = sqrt(eps)
  end
  df = 1/h * (f(x+h) - f(x)) % Calcolo della derivata
else

• …Ma il secondo parametro è f stessa!

Alcuni algoritmi utilizzano funzioni come parametri

Funzioni come Parametri

In Matlab si può fare:

In derive, trattiamo un parametro come un nome di funzione

function df = derive(f, x)
  if abs(x) > 1e-6 % Scelta di h
    h = sqrt(eps) * x;
  else
    h = sqrt(eps)
  end
  df = 1/h * (f(x+h) - f(x)) % Calcolo della derivata
else

• Notate che stiamo invocando f (si riconosce dalla parentesi)
• f è una variabile locale, che contiene una funzione

Funzioni come Parametri

In Matlab si può fare:

Da qualche parte dobbiamo definire \(f\):

function y = f(x)
  y = ...
end

Quando invochiamo derive (e.g. con \(x=1\)) non possiamo usare:

derive(f, 1)

• Se lo facciamo, Matlab crede che vogliamo eseguire f…
• …Mentre noi vogliamo solo passarlo!

Funzioni come Parametri

In Matlab si può fare:

Da qualche parte dobbiamo definire \(f\):

function y = f(x)
  y = ...
end

Quando invochiamo derive dobbiamo usare una sintassi speciale:

derive(@f, 1)

• La @ dice a Matlab che f non va eseguita…
• …Ma va “passata così com’è”

Funzioni come Parametri

Complessivamente abbiamo:

derive(f, 1) % Invocazione

function y = f(x) % Funzione da derivare
  y = ...
end

function df = derive(f, x) % Approssimazione della derivata
  df = ...
end

Come al solito, trovate il codice nello start-kit

Funzioni Anonime

Supponiamo di vole derivare:

\[f(x) = x^2 \log x\]

• A rigore, dovremmo definire:

function y = f(x)
  y = x.^2 .* log(x);
end

• Si può fare, ma è scomodo per una funzione così semplice!

Matlab ci fornisce un costrutto più compatto: le funzioni anonime

Funzioni Anonime

Si tratta di un modo alternativo per definire una funzione

La sintassi è:

@(<p1>, <p2>, ...) <espressone>

Il costrutto restituisce una funzione senza nome:

• <p1>, <p2>… sono i parametri formali
• La funzione denota il valore di <espressione>

Si può memorizzare la funzione in una variabile, e.g.:

f = @(x) x.^2 .* log(x);

• Inserisce nella variabile f…
• …Una funzione che, quando invocata, restituisce x^2

Funzioni Anonime

In prima battuta, potremmo pensare di scrivere:

f = @(x) x.^2 .* log(x);
derive(@f, 1)

In realtà, non funziona!

• La ragione è che f è già una variabile che contiene una funzione
• Quindi non c’è bisogno di dirlo di nuovo a Matlab

La forma corretta è quindi semplicemente:

f = @(x) x.^2 .* log(x);
derive(f, 1)  % Niente @!

Funzioni Anonime ed Ambienti

A differenza della funzioni “normali”…

Le funzioni anomime hanno accesso alle variabili dell’ambiente in cui sono definite

Per esempio:

a = 9;
f = @(x) a .* x.^2;

• Una funzione “normale” potrebbe accedere solo ad x (il parametro)
• Una funzione anonima può accedere anche ad a!

Un Caso d’Uso Importante

Consideriamo ancora l’oscillatore (discretizzato) di Van Der Pol:

\[\begin{align} x^{(t+1)} &= x^{(t)} + h y^{(t)} \\ y^{(t+1)} &= y^{(t)} + h \left(\mu (1 - x^{(t)2})y^{(t)} - x^{(t)}\right) \\ \end{align}\]

…Ed il suo codice di simulazione:

X = [];
T = 1:1000; % Istanti di tempo
xc = [x0, y0]; % Stato iniziale
for t = T
    X(t, :) = xc; % Salvo lo stato corrente
    xc = f(xc, h, mu); % Genero lo stato futuro
end

• Lo abbiamo usato in tutti gli esercizi seguenti, e non è buona cosa

Funzioni come Argomenti

Per essere “puliti”, dovremmo definire una funzione

Per prima cosa, incapsuliamo il codice in una nuova funzione:

function X = simulate(...)
  X = [];
  T = 1:1000;
  xc = [x0, y0];
  for t = T
      X(t, :) = xc;
      xc = f(xc, h, mu);
  end
end

Funzioni come Argomenti

Per essere “puliti”, dovremmo definire una funzione

Quindi, identifichiamo i parametri:

function X = simulate(..., T, ...)
  X = [];
  xc = [x0, y0];
  for t = T
      X(t, :) = xc;
      xc = f(xc, h, mu);
  end
end

• È bene che T sia un parametro…
• …Così possiamo definirlo al momento della chiamata

Funzioni come Argomenti

Per essere “puliti”, dovremmo definire una funzione

Quindi, identifichiamo i parametri:

function X = simulate(f, T, X0)
  X = [];
  xc = X0;
  for t = T
      X(t, :) = xc;
      xc = f(xc, h, mu);
  end
end

• Lo stesso vale per lo stato iniziale X0…
• …Ed a maggior ragione per la funzione di transizione f

Funzioni come Argomenti

Per essere “puliti”, dovremmo definire una funzione

Ci rimane ancora un problema:

function X = simulate(f, T, X0)
  X = [];
  xc = X0;
  for t = T
      X(t, :) = xc;
      xc = f(xc, h, mu); % <--- QUI!!
  end
end

• h e mu sono specifici per il nostro oscillatore…
• Finché appaiono nel codice, la nostra simulate non è davvero generica

Funzioni come Argomenti

Soluzione 1: includere h e mu nella definizione della funzione

function X = simulate(f, T, X0)
  X = [];
  xc = X0;
  for t = T
      X(t, :) = xc;
      xc = f(t, xc); % Passo solo lo stato
  end
end

• Passo anche il tempo t, è utile per alcuni sistemi…
• …E non è specifico di un particolare sistema

Funzioni come Argomenti

Soluzione 1: includere h e mu nella definizione della funzione

A parte avremo:

function xf = vdp(t, xc)
    h = 0.1; % Hard-coded nella funzione
    mu = 1; % Hard-coded nella funzione
    x = xc(1);
    y = xc(2);
    xf(1) = x + h * y;
    xf(2) = y + h * (mu * (1 - x^2)*y - x);
end

Funzioni come Argomenti

Soluzione 1: includere h e mu nella definizione della funzione

Nel complesso, potremmo avere:

T = 1:300;
X0 = [0.5, 0.5];
X = simulate(@vdp, T, X0); % Funzione come valore

function xf = vdp(t, xc)
    ...
end

Funziona, ma ha dei grossi difetti:

• h e mu sono hard-coded nella funzione vdp…
• …Se vogliamo provare valori diversi, dobbiamo ridefinire la funzione!

Funzioni Anonime e Funzioni Normali

Soluzione 2: usare una funzione anonima

Partiamo dalla versione corrente del codice:

function es_vdp()
    T = 1:300;
    X0 = [0.5, 0.5];
    X = simulate(@vdp, T, X0);
end

function xf = vdp(t, xc)
    h = 0.1;
    mu = 1;
    ...
end

Funzioni Anonime e Funzioni Normali

Soluzione 2: usare una funzione anonima

Ridefiniamo vdp in modo che riceva solo i parametri appropriati

function es_vdp()
    h = 0.1; % Spostato
    mu = 1; % Spostato
    T = 1:300;
    X0 = [0.5, 0.5];
    X = simulate(@vdp, T, X0);
end

function xf = vdp(xc, h, mu) % Parametri cambiati
    ...
end

Funzioni Anonime e Funzioni Normali

Soluzione 2: usare una funzione anonima

Definiamo una funzione anonima con l’interfaccia richiesta da simulate…

function es_vdp()
    h = 0.1; % Spostato
    mu = 1; % Spostato
    T = 1:300;
    X0 = [0.5, 0.5];
    f = @(t, x) ...; % Parametri corretti per "simulate"
    X = simulate(@vdp, T, X0);
end

function xf = vdp(xc, h, mu)
    ...
end

Funzioni Anonime e Funzioni Normali

Soluzione 2: usare una funzione anonima

…E che non faccia altro che chiamare vdp

function es_vdp()
    h = 0.1; % Spostato
    mu = 1; % Spostato
    T = 1:300;
    X0 = [0.5, 0.5];
    f = @(x, t) vdp(x, h, mu); % Chiama solo vdp!
    X = simulate(@vdp, T, X0);
end

function xf = vdp(xc, h, mu)
    ...
end

Funzioni Anonime e Funzioni Normali

Soluzione 2: usare una funzione anonima

function es_vdp()
    h = 0.1; % Spostato
    mu = 1; % Spostato
    T = 1:300;
    X0 = [0.5, 0.5];
    f = @(x, t) vdp(x, h, mu); % Chiama solo vdp!
    X = simulate(@vdp, T, X0);
end

Quando f viene eseguita, invoca vdp(x, h, mu)

• x è uno dei parametri di f, ma h e mu no
• Matlab li cerca nell’ambiente in cui f è definita!

Un Pattern

Useremo molto spesso le funzioni anonime in questo modo:

f = @(x, t) ftransition(x, ...)
X = simulate(f, ...)

function xf = ftransition(x, ...)
    ...
end

• Così ftransition ha solo i suoi parametri “naturali”…
• La funzione anonima f la “avvolge” (fa da wrapper)…
• …Ed espone l’interfaccia richiesta da simulate

Come al solito, trovate il codice nello start-kit

Esercizio: Oscillatore di Van Der Pol Forzato

Consideriamo una variante dell’oscillatore di Van Der Pol

In particolare, vediamo la versione discretizza e “forzata”:

\[\begin{align} x^{(t+1)} &= x^{(t)} + h y^{(t)} \\ y^{(t+1)} &= y^{(t)} + h \left(\mu (1 - x^{(t)2})y^{(t)} - x^{(t)} - A \sin(\omega h t) \right) \\ \end{align}\]

Il termine \(A \sin(\omega h t)\) si dice guida (driver):

• \(A\) è l’ampiezza dell’oscillazione guida
• \(\omega\) è la sua frequenza
• \(t\) è il tempo
• \(h\) compare perché il tempo è discretizzato

Il valore della guida non dipende dallo stato, ma solo dal tempo

Oscillatore di Van Der Pol Forzato

Partendo dal file es_forced_vdp.m nello start-kit:

• Definite la funzione di transizione per l’oscillatore forzato:

function Xf = forced_vdp(X, t, omega, A, h, mu)

• Aggiungete il codice di simulazione
  • Aggiungete una funzione anonima, se necessario

Confrontate i risultati con l’oscillatore “normale” (in es_dp.m):

• Disegnate l’andamento di \(x\) nel tempo
• Disegnate la traiettoria (i.e. insieme dei valori di \(x\) e \(y\) visitati)

Come differiscono i due andamenti? E le due traiettorie?

Esercizio: Random Walk

Ricordate il nostro esempio di random walk 1D?

Formalmente, era caratterizzato dalla ricorsione:

\[x^{(t+1)} = x^{(t)} + d\]

• Dove:

\[d = \left\{\begin{aligned} & +1 & \text{ con probabilità } p \\ & -1 & \text{ altrimenti} \end{aligned}\right.\]

Nel file es_walk.m è definita la funzione di transizione, con interfaccia:

function xf = onestep(t, xc, p)

• Simulate il sistema utilizzando simulate
  • Aggiungete una funzione anonima (se necessario)
• Stampate a video la posizione finale
• Disegnate l’andamento della posizione nel tempo

Esercizio: Random Walk Multiple

La nostra random walk è un esempio di sistema stocastico

• Il comportamento è soggetto ad incertezza
• Ogni simulazione può avere un esito diverso

Ma in media come si comporta il sistema?

Per determinarlo possiamo:

• Simulare molte volte il sistema…
• …E quindi studiare i risultati

Per esempio possiamo:

• Calcolare la posizione finale media
• Disegnare un istogramma

Istogrammi

Un istogramma è un grafico che si ottiene nel modo seguente:

• Dato una collezione di valori \(x_i\)
• Si divide il dominio \(D\) in intervalli uguali
• Si conta quanti valori \(x_i\) cadono in ciascun intervallo
• Per ogni intervallo, sia \(c_j\) il valore del conteggio
• Si disegnano su un grafico a barre i valori di \(c_j\)

Istogrammi

Un esempio (l’altezza di un neonato, campione di 200 valori)

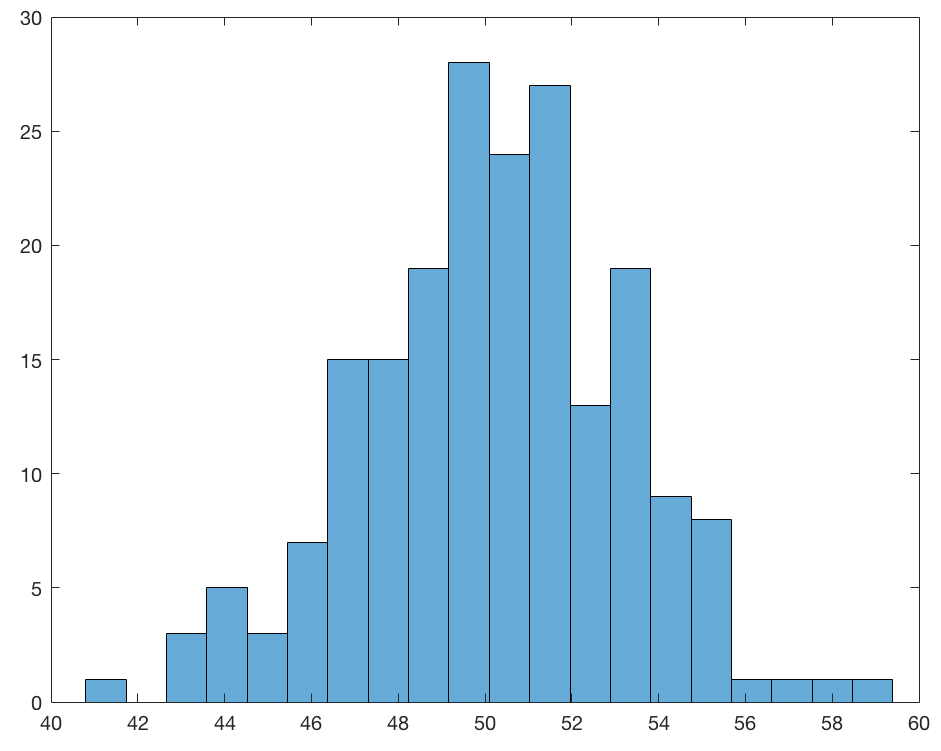
Istogrammi

Un istogramma è un grafico che si ottiene nel modo seguente:

• Dato una collezione di valori \(x_i\)
• Si divide il dominio \(D\) in intervalli uguali
• Si conta quanti valori \(x_i\) cadono in ciascun intervallo
• Per ogni intervallo, sia \(c_j\) il valore del conteggio
• Si disegnano su un grafico a barre i valori di \(c_j\)

In Matlab potete usare:

histogram(X)    % X = vettore con i valori
histogram(X, M) % M = numero di intervalli

• Di default, Matlab calcola da solo quali intervalli usare

Esercizio: Random Walk Multiple

Nel file es_many_walks.m

• Simulare la nostra random walk \(N\) volte
• Memorizzare in un vettore tutte le posizioni finali raggiunte
• Disegnare un istogramma

Come varia l’istogramma al variare di \(p\)?

Esercizio: arrayfun

Matlab fornisce la funzione:

function y = arrayfun(f, x)

• Che applica la funzione f ad ogni elemento nel vettore x…
• …E restituisce i risultati in y

Nel file es_arrayfun.m si definisca una funzione:

function y = my_arrayfun(f, x)

…Che replichi il comportamento di quella di Matlab

• La funzione \(f\) da utilizzare per il testing è fornita nello start-kit
• Si disegni il grafico di \(f\) nell’intervallo \([-2, 2]\)

Esercizio: Random Surfer

Consideriamo un semplice modello per un utente web

Il nostro utente si comporta così:

• Parte da una pagina scelta uniformemente a caso
• Ad ogni passo:
  • Con probabilità \(1-p\) l’utente clicca su un link a caso
  • Con probabilità \(p\) l’utente si stanca…
  • …E ricomincia da una pagina a caso
• Se non ci sono link in uscita, l’utente resta fermo

Esercizio: Random Surfer

Consideriamo un semplice modello per un utente web

Possiamo descrivere la rete come un grafo, e.g.:

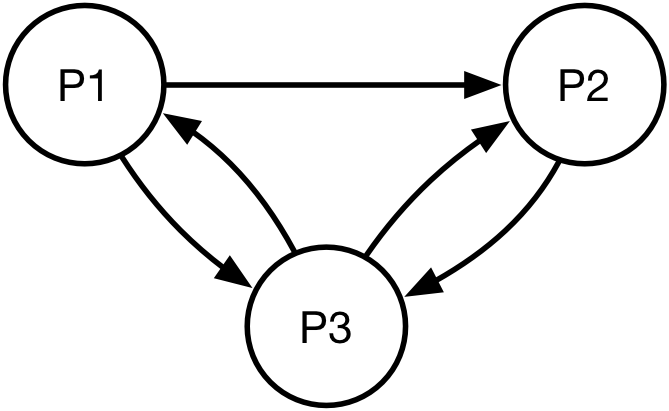
• I nodi (i.e. le palline) rappresentano pagine
• Gli archi (i.e.) le freccette rappresentano i link
• Supponiamo di avere \(n\) pagine
• Chiamiamo \(P_{i,j}\) la probabilità di cliccare sul link da \(j\) a \(i\)
  • Quindi, \(P_{i,j} = 1 / (\text{num. link in uscita da } j)\)

Esercizio: Random Surfer

Proviamo a tradurlo in equazioni

Per lo stato, facciamo una scelta un po’ strana:

• Una variabile \(x_i\) per ogni pagina, con \(x_i \in [0, 1]\)
• \(x_i\) rappresenta la probabilità che l’utente sia sulla pagina \(i\)

All’inizio, tutte le pagine sono equiprobabili:

• Quindi, per tutte le pagine \(x_i = 1/n\)

Esercizio: Random Surfer

Proviamo a tradurlo in equazioni

Calcolare lo stato futuro vuol dire:

• A partire delle probabilità \(x_i^{(t)}\) di essere sulla pagina \(i\)…
• …Calcolare le probabilità future \(x_i^{(t+1)}\)

Formalmente, la probabilità \(x_i^{(t)}\) di essere su \(i\) al passo \(t+1\):

\[x_i^{(t+1)} = \underbrace{p}_{\text{mi stanco}} \overbrace{\frac{1}{n}}^{\text{reset}} + \underbrace{(1-p)}_{\text{non mi stanco}} \sum_{j = 1}^n \overbrace{x_j^{(t)}}^{\text{sono su $j$}} \underbrace{P_{i,j}}_{\text{link per $i$}}\]

• È data dalla probabilità di finire su \(i\) dopo essersi stancati…
• …Più la probabilità di non stancarsi e finire su \(i\) da un’altra pagina

Esercizio: Random Surfer

Se ci fate caso, la funzione di transizione è lineare

Per i sistemi dinamici lineari, è comodo usare la notazione matriciale:

\[x^{(t+1)} = p \frac{1}{n} + (1-p) P x^{(t)}\]

• \(x^{(t+1)}\) è il vettore (colonna) delle probabilità al tempo \(t+1\)
• \(x^{(t)}\) è il vettore (colonna) delle probabilità al tempo \(t\)
• \(P\) è la matrice con le probabilità di transizione \(P_{i,j}\)

Vogliamo definire un simulatore per il modello appena visto

Esercizio: Random Surfer

Il file es_surfer.m nello start-kit:

Definisce la funzione:

function xf = browse(xc, P, p, n)

..Che implementa la ricorsione:

\[x^{(t+1)} = p \frac{1}{n} + (1-p) P x^{(t)}\]

• La formula matriciale assume che \(x^{(t)}\) sia una colonna…
• …Mentre il vettore di stato è una riga
• Questo rende necessarie alcune trasposizioni

Definite il codice di simulazione:

• Disegnate su un’unica figure l’andamento di \(x_0\), \(x_1\), \(x_2\) nel tempo
  • Quali sono alla fine le pagine su cui è più probabile trovarsi?

Esercizio: Random Surfer

Le probabilità finali:

• Rappresentano la probabilità di visita delle pagine
• Si potrebbero usare per capire quali pagine sono più importanti

È esattamente quello per cui il modello di esempio è nato!

Sapete chi l’ha inventato?

BTW: l’algoritmo si chiama pagerank

Esercizio: Previsioni del Tempo

Vogliamo utilizzare un sistema dinamico per prevedere il tempo

Supponiamo che (sommariamente) valgano le regole seguenti:

• Se un giorno c’è bel tempo
  • Il giorno successivo sarà bello con il 90% di probabilità
  • Il giorno successivo sarà brutto con il 10% di probabilità
• Se un giorno c’è brutto tempo
  • Il giorno successivo sarà bello con il 50% di probabilità
  • Il giorno successivo sarà brutto con il 50% di probabilità

Esercizio: Previsioni del Tempo

Per lo stato, ragioniamo di nuovo in termini di probabilità:

• \(x_g^{(t)}\) = probabilità che il tempo sia bello a \(t\)
• \(x_b^{(t)}\) = probabilità che il tempo sia brutto a \(t\)

Per le transizioni, avremo:

\[\begin{align} x_g^{(t+1)} = x_g^{(t)} P_{g,g} + x_b^{(t)} P_{g,b} \\ x_b^{(t+1)} = x_g^{(t)} P_{b,g} + x_b^{(t)} P_{b,b} \end{align}\]

• \(P_{g,b}\) è la probabilità che il tempo sia brutto a \(t\) e bello a \(t+1\), etc.
• Il sistema è di nuovo lineare. In forma matriciale possiamo scrivere:

\[x^{(t+1)} = P x^{(t)} \quad \text{ con: } P = \left(\begin{array}{cc} P_{g,g} & P_{g,b} \\ P_{b,g} & P_{b,b} \\ \end{array}\right) \]

Esercizio: Previsioni del Tempo

Si parta dal file es_weather.m nello start-kit

Si definisca la funzione di transizione:

function xf = day(xc, P)

• Dove xc è lo stato corrente (\(x_g^{(t)}, x_b^{(t)}\))…
• …E P è la matrice \(P\) di transizione…
• …Che deve essere definita come parte dell’esercizio

Si sviluppi il codice di simulazione:

• Si disegni l’andamento delle due probabilità (bel tempo/brutto tempo)
  • Nel codice, si assume inizialmente che il primo giorno sia brutto
  • In un secondo momento, provate l’alternativa opposta

Esercizio: Crescita Logistica

Sia data una popolazione che segue il modello logistico

\[x^{(t+1)} = r\, ^{(t)} \left(1 - \frac{x^{(t)}}{N}\right)\]

Dove:

• \(r\) indica il tasso di crescita (deve valere \(r > 1\))
• \(N\) indica un valore di popolazione…
• …che, se raggiunto, ne causa il collasso immediato

Vogliamo studiare il comportamento del modello mediante simulazione

Esercizio: Crescita Logistica

A partire dal file es_logi.m nello start-kit:

Definite la funzione di transizione:

function xf = logi(xc, r, k)

• Che calcoli lo stato futuro xf
• …A partire da quello corrente xc, e dai valori di r e k

Definite il codice di simulazione:

• Lo stato iniziale è definito nel codice (e così l’intervallo di simulazione)
• Valori di partenza per r e k sono definiti nel codice
• Si disegni l’andamento dello stato nel tempo
• Si esplori cosa succede per vari valori di \(r\), da \(1.1\) a \(4.0\)

Esercizio: Un Modello Preda-Predatore

I modelli preda-predatore:

• Rappresentano la co-evoluzione di due popolazioni antagoniste
• E.g. prede-predatori, ma anche reazioni chimiche che si ostacolano

Tipicamente ci sono due elementi nel vettore dello stato:

• Il numero di “prede” \(H\)
• Il numero di “predatori” \(P\)

Simulando il sistema:

• Si può studiare il comportamento delle due popolazioni
• Si può verificare se vi sia un equilibrio stabile

Esercizio: Un Modello Preda-Predatore

Consideriamo questo modello preda-predatore:

\[\begin{align} & H^{(t+1)} = \overbrace{r \left(1 - \frac{H^{(t)}}{k} \right) H^{(t)}}^{\text{crescita logistica}} - \overbrace{s\, H^{(t)} P^{(t)}}^{\text{prede eliminate}} \\ & P^{(t+1)} = \underbrace{u\, P^{(t)}}_{\text{calo in assenza di prede}} + v \underbrace{\left( s\, H^{(t)} P^{(t)} \right)}_{\text{prede eliminate}} \end{align}\]

• \(k\) è la massima popolazione di prede sostenibile
• \(s\) è la frazione di \(H^{(t)}\) che un predatore può “mangiare”
• \(u < 1\) è il ritmo di scomparsa dei predatori in assenza di prede
• \(v\) è il “bonus riproduttivo” per ogni preda “mangiata”

Esercizio: Un Modello Preda-Predatore

Nello start-kit, partite dal file es_logi_pp.m

Implementare la funzione di transizione:

function xf = logi_pp(xc, r, k, s, u, v)

• HP: xc(1) sia il numero di prede e xc(2) quello di predatori
• I valori di \(r, k, s, u, v\) sono già definiti nel codice

Definite il codice di simulazione nella funzione principale:

• Lo stato iniziale è riportato nel codice
• Disegnate l’andamento delle due popolazioni nel tempo
• Disegnate la traiettoria nello spazio degli stati

Esercizio: Un Modello Preda-Predatore

Provate a fare delle variazioni!

Aumentate e diminuite (solo) \(s\):

• Cosa vi aspettate che succeda? Cosa succede?

Aumentate e diminuite (solo) \(r\):

• Cosa vi aspettate che succeda? Cosa succede?

Aumentate e diminuite (solo) \(u\):

• Cosa vi aspettate che succeda? Cosa succede?

Riuscite a spiegare intuitivamente le ragioni?

Esercizio: Gigi l’Ubriaco

Dopo una serata di bagordi, Gigi deve tornare a casa a piedi

• All’inizio, Gigi si muove in una data direzione (verso casa)
• Ad ogni passo, Gigi mantiene la direzione con probabilità \(p\)
• Oppure cambia direzione, con probabilità \(1-p\)

Intuitivamente \(p\) controlla il livello di sobrietà

• Con \(p = 1\) Gigi è sobrio: cammina sicuro verso casa
• Con \(p = 0.5\) Gigi ha bevuto più di qualche bicchiere di troppo…

Vogliamo osservare il moto di Gigi nel tempo

• Lo faremo modellando il moto come un sistema dinamico
• Usiamo un approccio stocastico (numeri pseudo-casuali)

Esercizio: Gigi l’Ubriaco

Cosa è lo stato \(x^{(t)}\) per il nostro problema?

Lo \(X^{(t)}\) deve contenere abbastanza informazioni per determinare \(X^{(t+1)}\)

• Quindi ci serve la posizione di Gigi
• Ma anche la direzione dell’ultimo movimento!

Lo stato è un vettore di due componenti:

\[X = (x, d)\]

…E vale la ricorsione:

\[\begin{align} & d^{(t+1)} = \left\{\begin{aligned} & d^{(t)} & \text{ con probabilità } p \\ & -d^{(t)} & \text{ altrimenti } \end{aligned}\right.\\ & x^{(t+1)} = x^{(t)} + d^{(t+1)} \end{align}\]

Esercizio: Gigi l’Ubriaco

A partire dal file es_drunkard.m nello start-kit:

Definite la funzione di transizione:

function xf = f(t, xc)

• HP: xc(1) = posizione, xc(2) direzione dell’ultimo spostamento

Simulate l’andamento della posizione di Gigi nel tempo:

• Visualizzate come si evolve lo stato nel tempo
• L’andamento sembra più o meno realistico della nostra random walk originale?
• Cosa succede cambiando \(p\)?

Esercizio: Provaci ancora, Gigi!

Proviamo a studiare il “comportamento medio” di Gigi:

Nel file es_many_drunkards.m, come nel caso della random walk:

• Simulare \(N\) camminate
• Memorizziamo in un vettore tutte le posizioni finali raggiunte
• Disegniamo un istogramma

Come varia l’istogramma al variare di \(p\)?

Esercizio: Trovare Elementi in un Vettore

Nel file di funzione es_findidx.m, definire la funzione:

function I = my_findidx(X, V)

• Con X scalare e V vettore, che restituisca nel vettore I…
• …Gli indici degli elementi che in V sono uguali a X

Per esempio:

V = [1, 2, 4, 2];
my_findidx(2, V)  % Denota [2, 4]

• Si implementi la funzione utilizzando un ciclo for

Esercizio: Trovare Elementi in un Vettore

Si verifichi la correttezza nella funzione principale es_findidx:

• Si utilizzino dei vettori di numeri interi casuali, ottenuti con randi

Come ottenere lo stesso risultato con le funzioni predefinite?

• Si determini un metodo e lo si sfrutti per fare un confronto
• Suggerimento: vi ricordate della funzione find?

Esercizio: Prodotto Matriciale

Nel file di funzione es_mprod.m, si definisca la funzione:

Si definisca una funzione:

function Z = my_mprod(A, B)

• Che calcoli il prodotto matriciale di A e B

Si verifichi la correttezza:

• Nella funzione principale
• Utilizzando matrici di numeri casuali (attenzione alle dimensioni!)
• Confrontandosi con l’operatore di prodotto in Matlab

Suggerimento: ogni prodotto riga/colonna è un prodotto scalare!

Esercizio: Scorrimento Circolare

Nel file di funzione es_shift.m, definite la funzione:

function W = my_shift(V)

• Deve restituire un vettore W, identico a V…
• …Ma con gli elementi spostati a sx di una posizione…
• …E in modo circolare: il primo elemento diventa l’ultimo

Per esempio:

my_shift([1, 2, 3, 4])  % Denota [2, 3, 4, 1]

Esercizio: Scorrimento Circolare

Verificate la correttezza:

• Utilizzate vettori casuali o inseriti a mano
• Controllate il risultato visivamente

Suggerimento:

• Si può implementare la funzione scambiando gli elementi consecutivi
• …Ossia scambiando W(ii) con W(ii+1) in sequenza