Limiti degli Script in Matlab

Supponiamo di avere il nostro algoritmo per \(\zeta(s)\) in uno script:

s = 3;
z = 0;
old_z = -1;
n = 1;
for i = 1:10000
  z = z + 1 ./ n.^s;
  if abs(z - old_z) < 1e-6
    break
  end
  old_z = z;
end

Limiti degli Script in Matlab

Supponiamo di avere il nostro algoritmo per \(\zeta(s)\) in uno script:

s = 3;
z = 0;
old_z = -1;
n = 1;
for i = 1:10000
  z = z + 1 ./ n.^s;
  if abs(z - old_z) < 1e-6
    break
  end
  old_z = z;
end

• Possiamo eseguirlo molte volte, ma sempre con s = 3
• Per cambiare s, dobbiamo modificare lo script
• Se \(\zeta(s)\) va valutata spesso, diventa molto scomodo

Limiti degli Script

I file di script sono utili per:

• Effettuare test
• Eseguire una analisi di dati specifici
• Risolvere un preciso problema numerico

Non sono adatti a definire un algoritmo riutilizzabile

Per tali casi possiamo definire una nuova funzione

• Una funzione è un sotto-programma (come uno script)
• Ma può ricevere dei parametri
• E può restituire un risultato

Stiamo usando funzioni già dalla prima lezione!

Definizione di Funzioni in Octave

Per definire una nuova funzione si usa la sintassi:

function <res> = <nome funz.>(<p1>, <p2>, ...)
  <corpo>
end

• <fn> è il nome della funzione
• <pXX> sono nomi di variabili (si chiamano parametri formali)
• <res> è il nome della variabile da restituire

Si chiama interfaccia di una funzione l’insieme del suo nome, dei parametri e delle variabili di ritorno

Definizione di Funzioni in Octave

Per definire una nuova funzione si usa la sintassi:

function <res> = <nome funz.>(<p1>, <p2>, ...)
  <corpo>
end

Usiamo come esempio la nostra Zeta di Riemann:

function z = zeta(s)
  ...
end

• La funzione si chiama zeta
• Riceve in ingresso un singolo parametro, internamente chiamato s
• Restituisce un singolo valore, internamente chiamato z

Semantica di una Chiamata a Funzione

Cosa succede quando eseguiamo (e.g.) zeta(3)+[INVIO]?

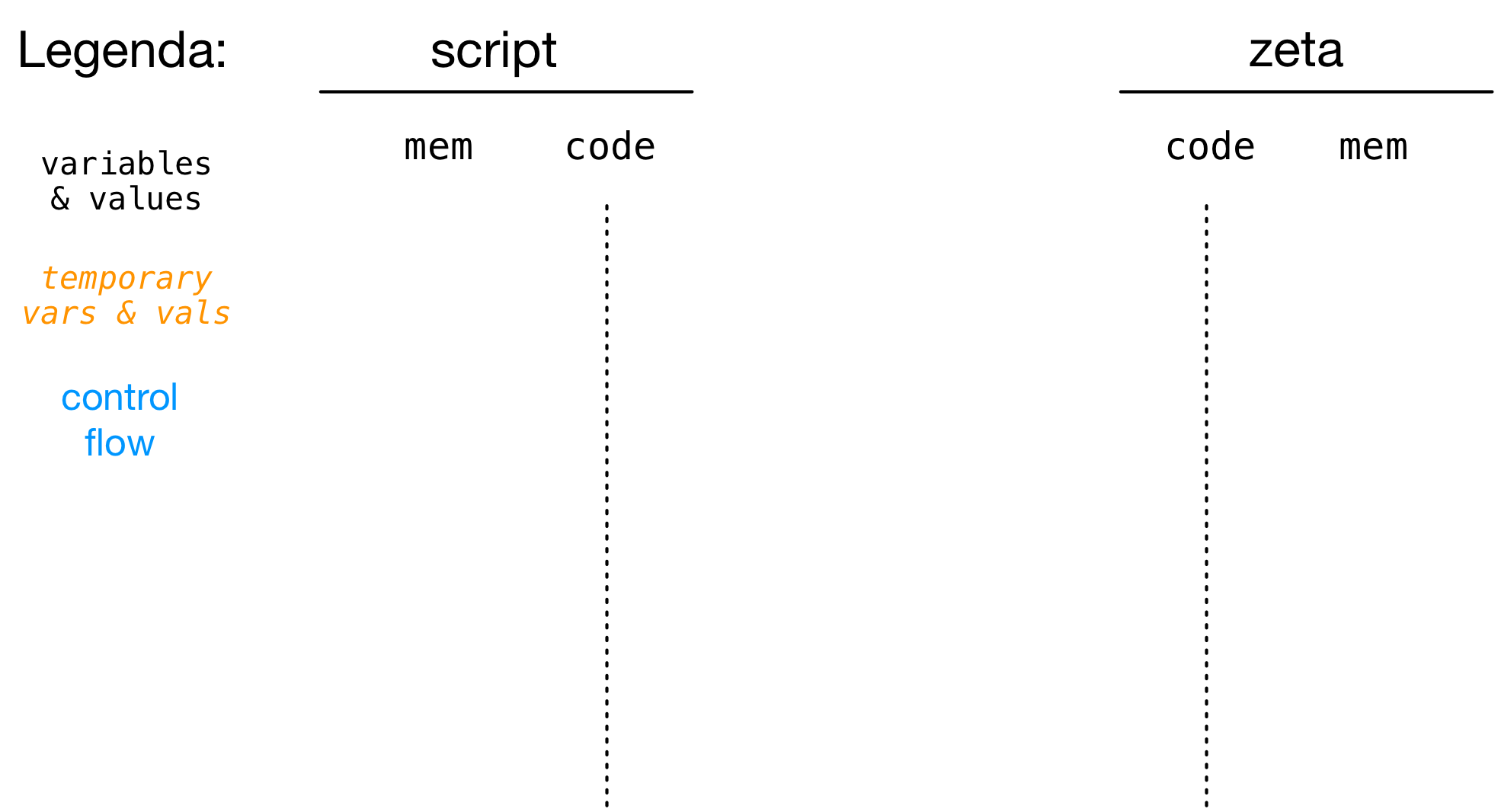
• Chiamante: lo script, chiamato: zeta

Semantica di una Chiamata a Funzione

Cosa succede quando eseguiamo (e.g.) zeta(3)+[INVIO]?

• Step 1: valutazione dei parametri nel chiamante (detti parametri attuali)

Semantica di una Chiamata a Funzione

Cosa succede quando eseguiamo (e.g.) zeta(3)+[INVIO]?

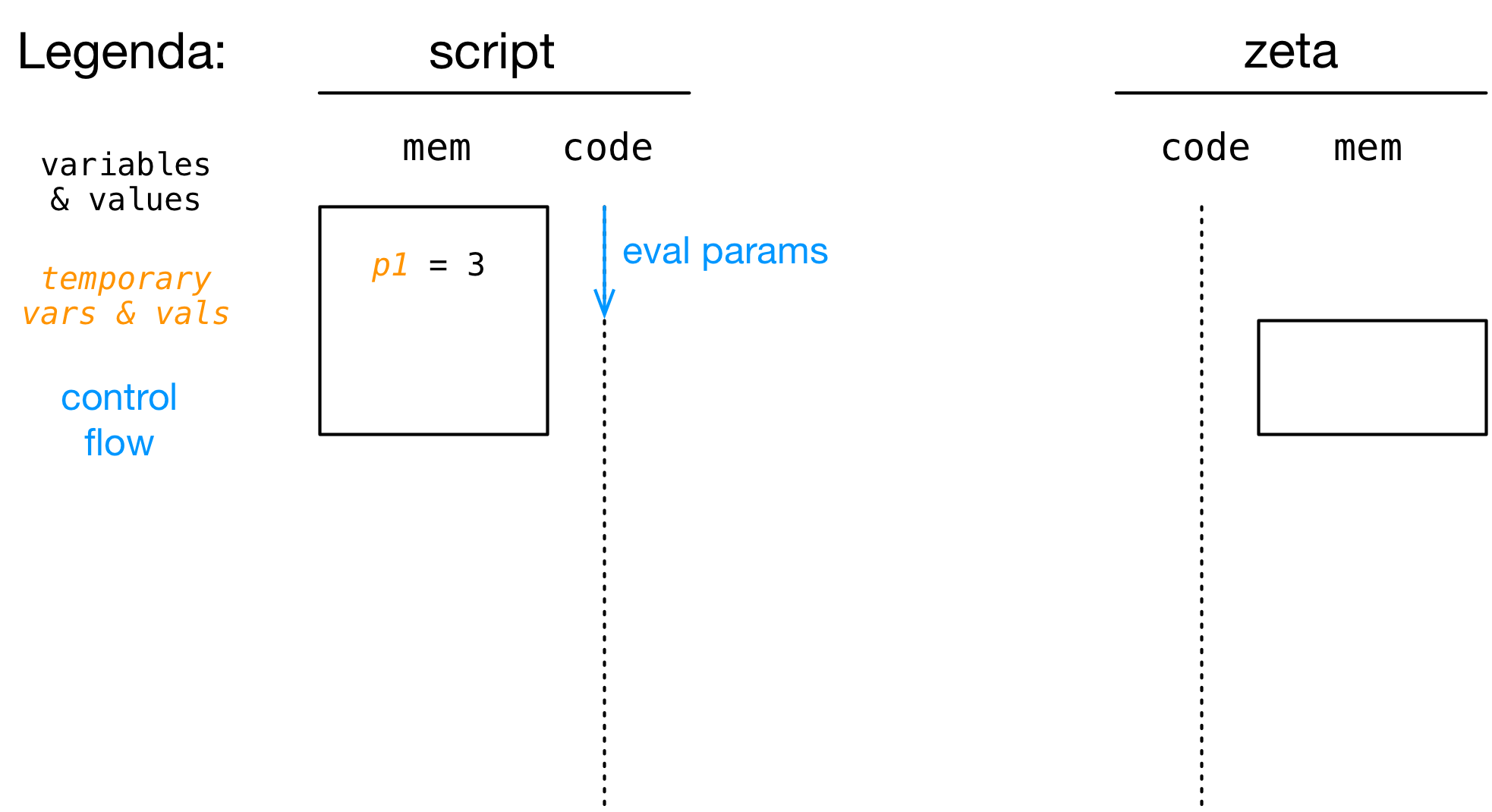
• Step 1: viene allocata memoria per la funzione (il suo record di attivazione)

Semantica di una Chiamata a Funzione

Cosa succede quando eseguiamo (e.g.) zeta(3)+[INVIO]?

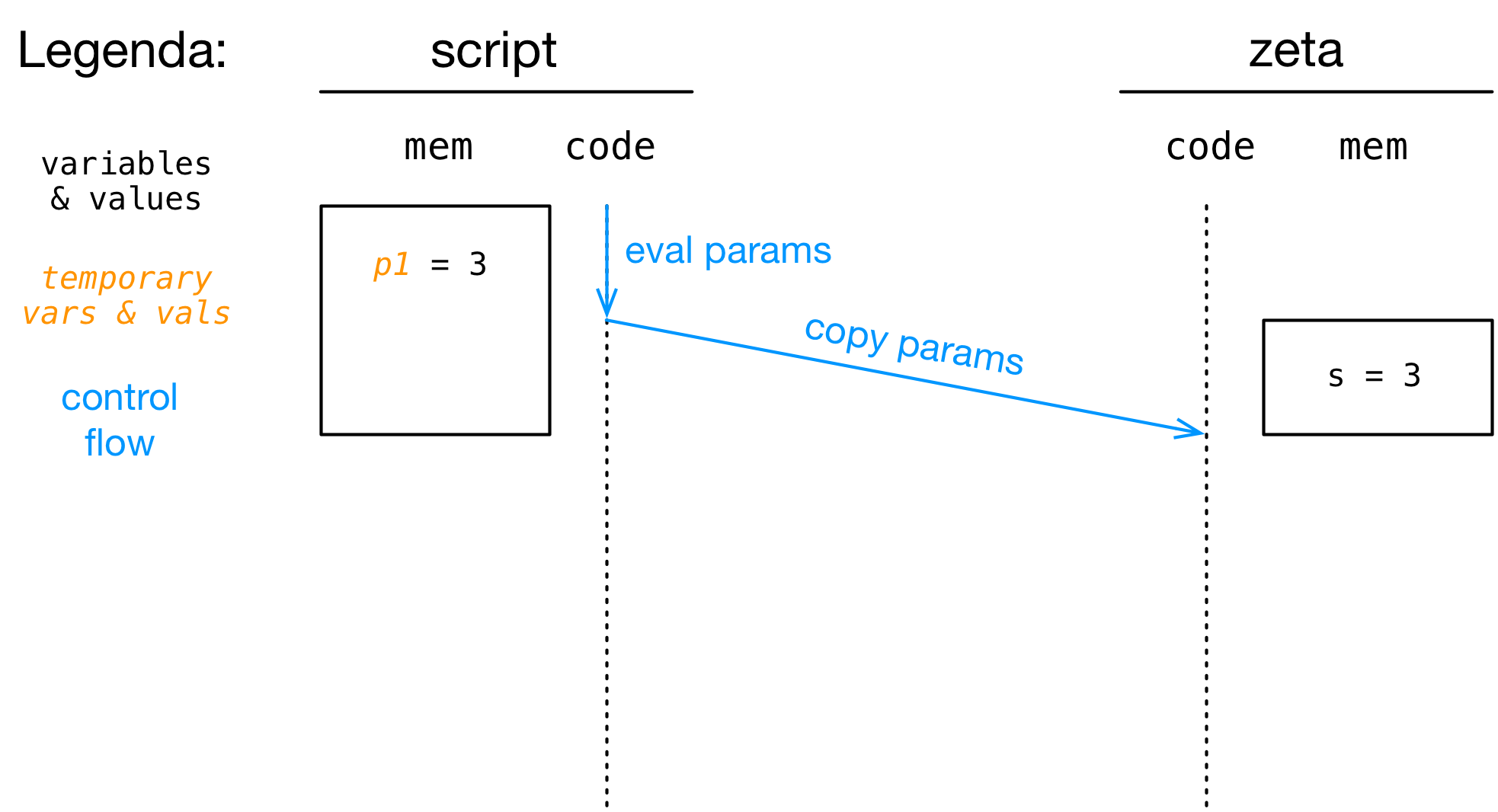
• Step 3: i valori dei parametri attuali sono copiati nei parametri formali

Semantica di una Chiamata a Funzione

Cosa succede quando eseguiamo (e.g.) zeta(3)+[INVIO]?

• Parametri formali = sono semplicemente delle variabili
• Il loro nome è specificato nell’interfaccia

Semantica di una Chiamata a Funzione

Cosa succede quando eseguiamo (e.g.) zeta(3)+[INVIO]?

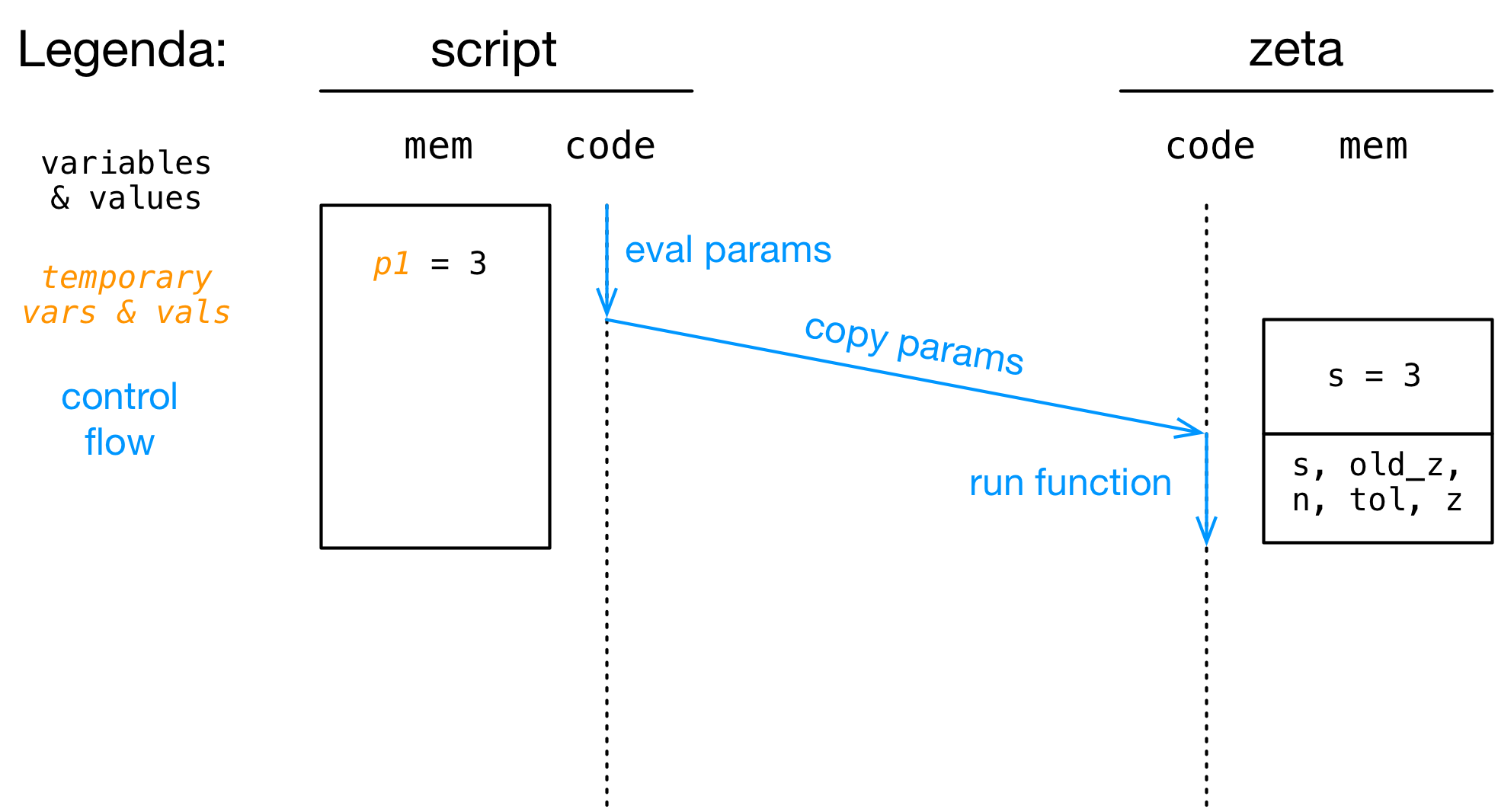
• Step 4: Viene eseguita la funzione

Semantica di una Chiamata a Funzione

Cosa succede quando eseguiamo (e.g.) zeta(3)+[INVIO]?

• Nota: le variabili della funzione sono definite nel suo record di attivazione

Semantica di una Chiamata a Funzione

Cosa succede quando eseguiamo (e.g.) zeta(3)+[INVIO]?

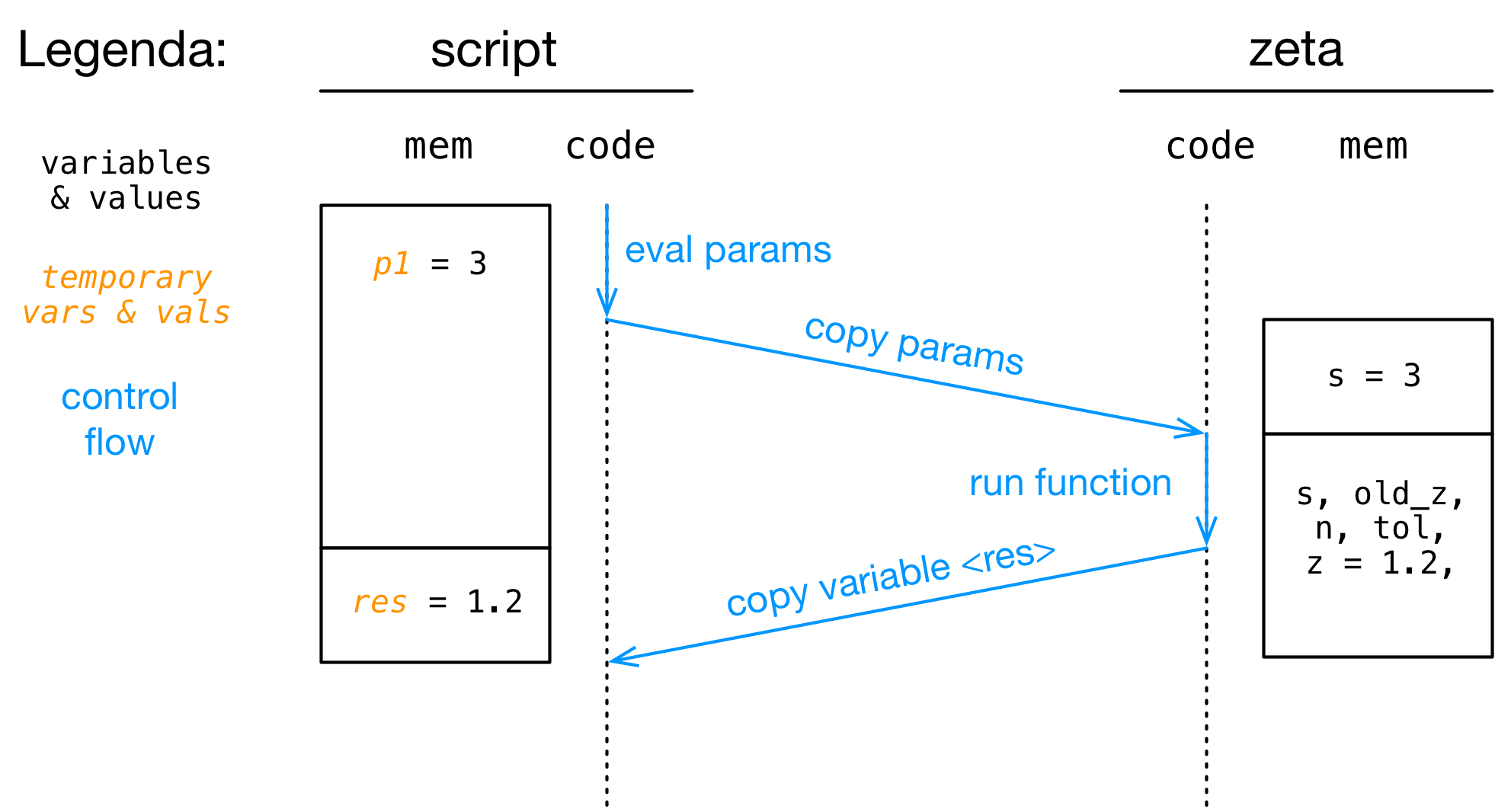
• Step 5: la funzione termina (z vale circa 1.2)

Semantica di una Chiamata a Funzione

Cosa succede quando eseguiamo (e.g.) zeta(3)+[INVIO]?

• Step 6: il valore di z (variabile di ritorno) viene copiato nel chiamante

Semantica di una Chiamata a Funzione

Cosa succede quando eseguiamo (e.g.) zeta(3)+[INVIO]?

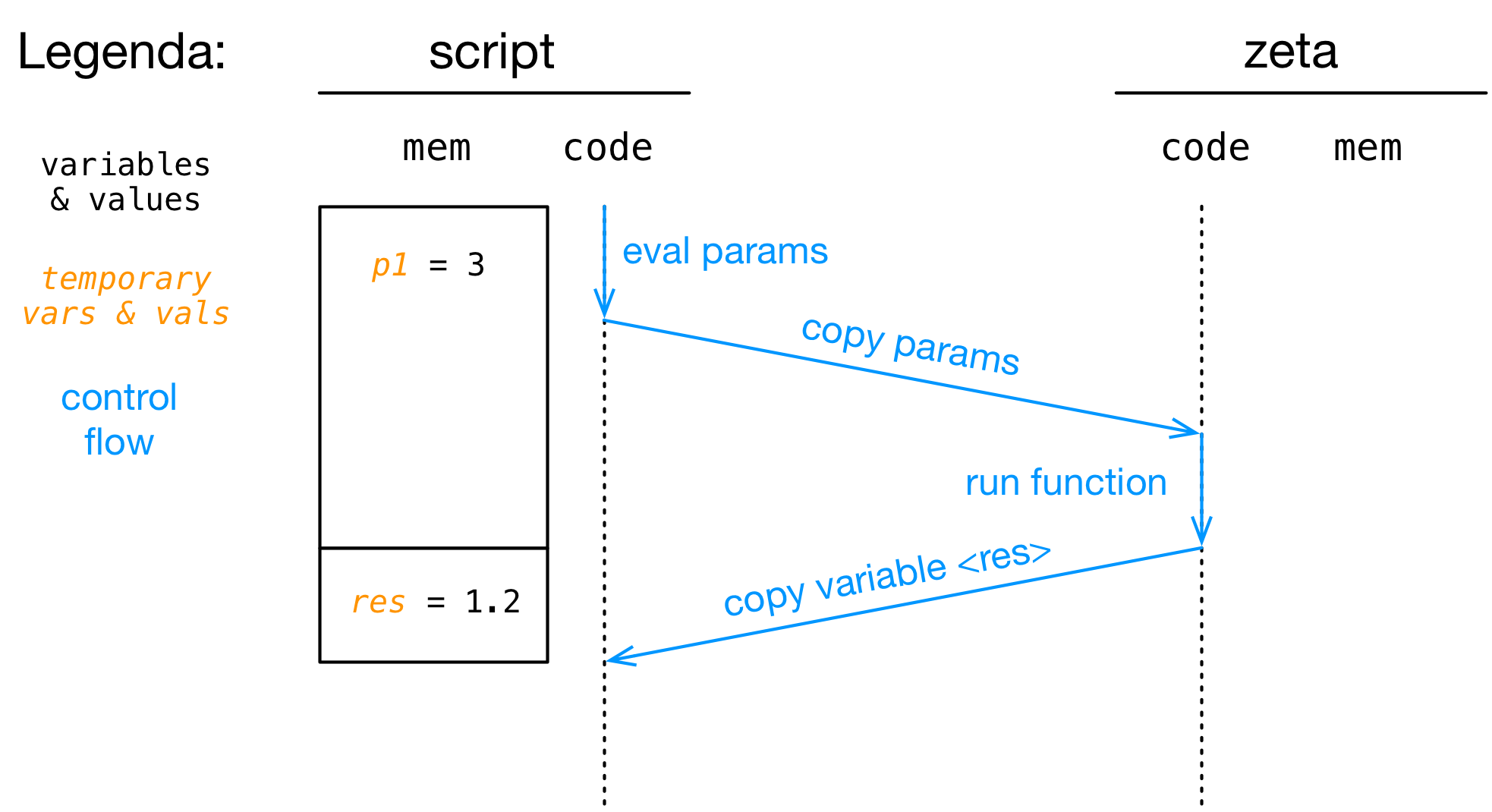
• Step 7: il record di attivazione viene distrutto

Semantica di una Chiamata a Funzione

Cosa succede quando eseguiamo (e.g.) zeta(3)+[INVIO]?

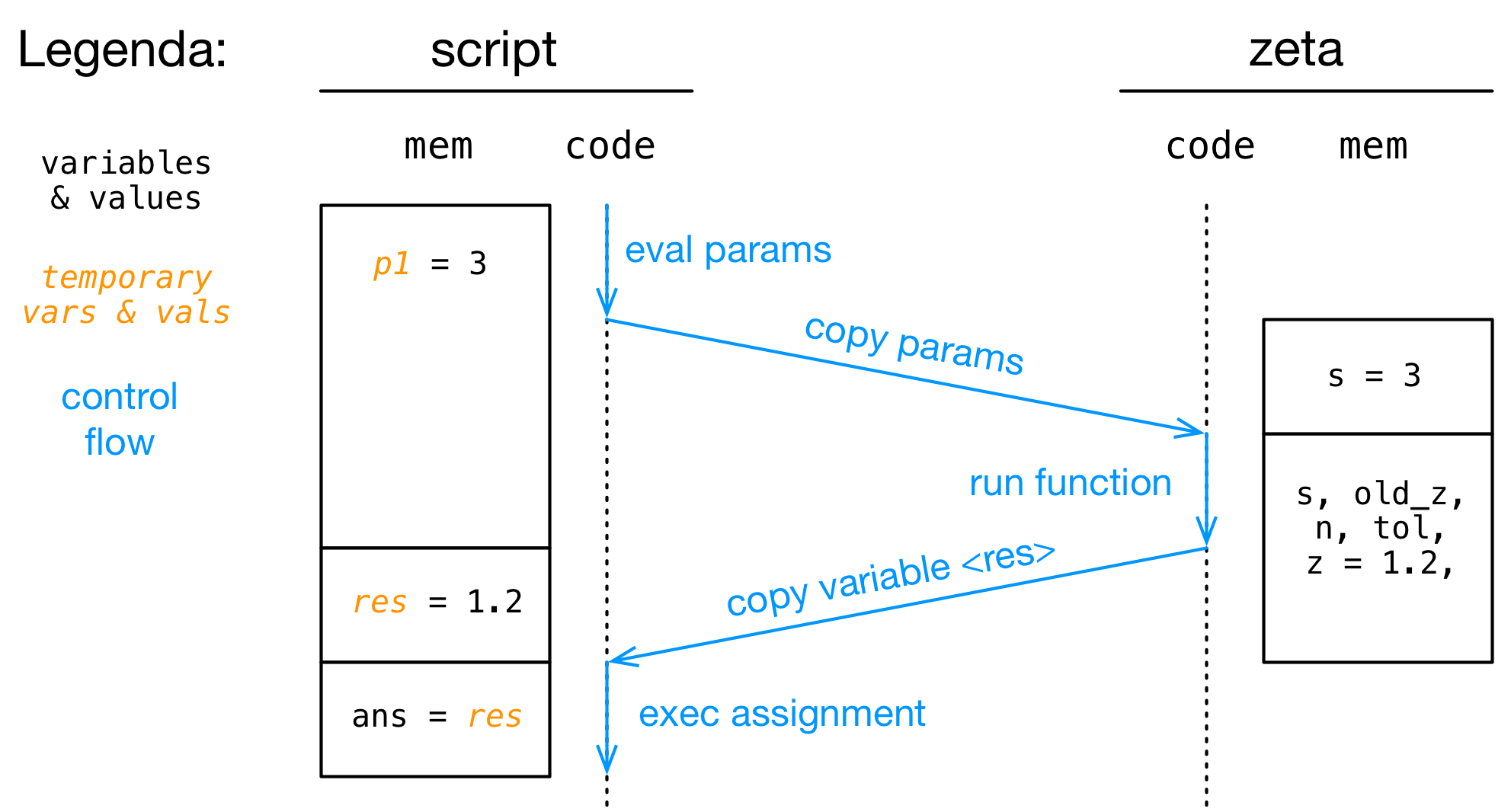
• In questo caso il risultato viene assegnato ad ans

Qualche Osservazione

Qualche considerazione, usando la nostra zeta come esempio:

function z = zeta(s)
  z = 0;
  old_z = -1;
  ...
end

Quando la funzione viene chiamata:

• Viene predisposto un spazio di memoria dedicato alla chiamata…
• …questo si chiama record di attivazione

Il record di attivazione viene distrutto quando il corpo della funzione termina

Qualche Osservazione

Qualche considerazione, usando la nostra zeta come esempio:

function z = zeta(s)
  z = 0;
  old_z = -1;
  ...
end

Le variabili definite all’interno della funzione (z, old_z…):

• Si dicono variabili locali
• Vengono allocate nel record di attivazione
• Quindi vengono distrutte quando la chiamata termina!

Qualche Osservazione

Qualche considerazione, usando la nostra zeta come esempio:

function z = zeta(s)
  z = 0;
  old_z = -1;
  ...
end

I parametri formali (s in questo caso) sono variabili locali:

• Vengono definite da Matlab al momento della chiamata
• Al loro interno viene inserito il valore dei parametri attuali

I parametri attuali (3 in zeta(3)) sono valori:

• Vengono ottenuti valutando le espressioni passate come argomento

Qualche Osservazione

Qualche considerazione, usando la nostra zeta come esempio:

function z = zeta(s)
  ...
end

zeta(3) % Un solo parametro, in questo caso

Il passaggio di parametri è posizionale:

• L’espressione passata come argomento i-mo…
• …Viene valutata e denota il parametro attuale i-mo…
• …Che viene copiato nel parametro formale i-mo

Qualche Osservazione

Qualche considerazione, usando la nostra zeta come esempio:

function z = zeta(s)
  ...
end

zeta()  % Manca il valore del parametro!!!

Se alcuni parametri attuali vengono omessi nella chiamata:

• Matlab non definisce i parametri formali corrispondenti
• Nella funzione, la variabile (e.g.) s non è disponibile
• Al primo tentativo di accesso, Matlab solleva un errore
  • Tipicamente: Not enough input arguments

Qualche Osservazione

Qualche considerazione, usando la nostra zeta come esempio:

function z = zeta(s)
  z = 0;
  old_z = -1;
  ...
end

La variabile di ritorno (in queso caso z)

• È una variabile locale
• Al termine della chiamata, il suo contenuto è restituito al chiamante
• Se ci siamo dimenticati di assegnarvi un valore…
• …Al chiamante non arriva nulla!

Qualche Osservazione

Qualche considerazione, usando la nostra zeta come esempio:

function z = zeta(s)
  ...
  if abs(z - old_z) < 1e-6 % chiamiamo "abs"!
  ...
end

Il corpo di una funzione può contenere una chiamata a funzione:****

• In questo caso l’intero processo si ripete
• Si predispone un record di attivazione per la nuova chiamata, etc.
• Succede di continuo!
• Ricordate: oersino gli operatori aritmetici sono funzioni!

Ambienti e Regole di Visibilità

Abbiamo visto che:

• Ogni chiamata a funzione ha il suo spazio di memoria
• Anche lo script principale ha un suo spazio di memoria

Questi spazi di memoria si chiamano ambienti. Vale la regola che:

Le variabili in un ambiente sono accessibili (visibili) solo per il codice “proprietario” dell’ambiente

In sintesi:

• Le variabili dello script sono visibili solo nello script
• Le variabili locali sono visibili solo nella funzione

Interazione con l’Ambiente Corrente

È possibile ispezionare l’ambiente corrente utilizzando i comandi:

who % stampa i nomi delle variabili definite
whos % stampa i nomi + altre informazioni

È possibile eliminare una variabile utilizzando:

clear <nome variabile>

Come abbiamo visto, eliminiamo tutte le variabili con:

clear all

Funzioni con Più Variabili di Ritorno

In Matlab, una funzione può avere più variabili di ritorno

function [<r1>, <r2>, ...] = <nome>(<p1>, <p2>, ...)
  <corpo>
end

• <r1>, <r2>, etc. sono nomi di variabili
• In questo caso, va assegnato un valore a tutte

La funzione può essere chiamata con:

[<r1>, <r2>, ...] = <nome>(<p1>, <p2>, ...)

• <r1>, <r2>, etc. sono altri nomi di variabili

Funzioni con Più Variabili di Ritorno

Un esempio: restituire la parte reale ed immaginaria

function [R, I] = split(N)
  R = real(N);
  I = imag(N);
end

Possiamo chiamarla con:

[R, imm] = split(2 + 4i)

• I nomi delle variabili “ricettacolo” R ed imm…
• …Possono essere scelti arbitrariamente

Non c’entrano con R ed I nella funzione!

Modalità di Chiamata Multiple

Se ci interessa solo la parte reale, va bene anche:

R = split(2 + 4i)

• Matlab si accorge che c’è solo una variabile “ricettacolo”…
• …Ed inizializza solo R

Quindi, ci possono essere molti modi di chiamare una funzione:

• Non sarà così per le nostre funzioni…
• …Ma è decisamente così per le funzioni predefinite!

Controllate la documentazione (help, doc) delle funzioni che usiamo!

Terminazione Immediata di una Funzione

Consideriamo una funzione per trovare 0 in una matrice

function trovato = find_zero(A)
  trovato = false;
  [m, n] = size(A)
  for i == 1:m
    for j == 1:n
      if A(i, j) == 0;
        trovato = true;
        break;
      end
    end
  end
end

• break interrompe il ciclo su j, ma non quello su i!

Terminazione Immediata di una Funzione

Consideriamo una funzione per trovare 0 in una matrice

function trovato = find_zero(A)
  trovato = false;
  [m, n] = size(A)
  for i == 1:m
    for j == 1:n
      if A(i, j) == 0;
        trovato = true;
        return; % INTERROMPE LA FUNZIONE
      end
    end
  end
end

• L’istruzione return interrompe immediatamente la funzione

Funzioni e File di Script

In Matlab \(>\) 2016b si può definire una funzione in un file di script

• La funzione deve comparire in fondo al file
• Non deve essere la prima istruzione (vedi prossime slides)

Un caso tipico:

clear all  % Prima istruzione, puliamo l'ambiente

Z = zeta(3) % Chiamata

% Definizione della funzione
function z = zeta(s)
  ...
end

File di Funzione

In alternativa, una funzione può essere inserita in un file a parte

In particolare, in Matlab si chiama file di funzione

• Un file di testo con estensione .m…
• …Che ha come prima istruzione la definizione della funzione…
• …E dovrebbe avere lo stesso nome della funzione che contiene

Per esempio, nel file zeta.m possiamo inserire:

function z = zeta(s)
  ...
end

In Matlab 2016a, questa è l’unica alternativa possibile

File di Funzione

Quando proviamo ad invocare (e.g.) zeta(3):

• Matlab cerca un file di nome “zeta.m”
• Se lo trova, legge la definizione della funzione e la esegue

La ricerca avviene all’interno di una serie di cartelle:

• Una di esse è sempre la cartella corrente
• È qui che possiamo mettere i nostri file di funzione

Attenzione ai nomi!

• Se definiamo una funzione sum in “sum.m”
• “Oscuriamo” la funzione sum di Matlab

Limitazioni di Matlab pre-2016b

Matlab pre-2016b non permette di definire funzioni in script

A però volte una funzione è utile solo per un determinato problema

• E.g. regressione lineare, definizione di equazioni non lineari…

In questo caso definire un file di funzione rende le cose più complicate

È possibile aggirare il problema?

Sì! Il modo più semplice consiste in:

• Trattare l’intero script come una funzione
• Definire la “vera” funzione come ausiliaria

Funzioni Ausiliarie

Matlab permette di definire più funzioni in un unico file

Per esempio, nel file somma_mat.m:

function s = somma_mat(M) % Funzione principale
    s = 0;
    for C = M
        s = s + somma_col(M);
    end
end
function s = somma_col(C) % Funzione _ausiliaria_
    s = 0;
    for v = C
        s = s + v;
    end
end

Funzioni Ausiliarie

Matlab permette di definire più funzioni in un unico file

La funzione principale:

• Compare come prima istruzione del file
• Si chiama come il file
• È l’unica a poter essere chiamata dall’esterno

Le funzioni ausiliarie:

• Compaiono dopo quella principale
• Possono avere un nome arbitrario
• Ne potete definire quante ne volete

Funzioni e Script in Matlab pre-2016b

Supponiamo di avere uno script del genere:

% Lo script vero e proprio
clear all
W = rand(1, 1000);
res = my_sum(W)

% Definizione di funzione
function s = my_sum(V)
    s = 0;
    for v in V
        s = s + v;
    end
end

Funzioni e Script in Matlab pre-2016b

Possiamo convertirlo in una funzione!

function my_test() % no parametri e valori di ritorno
    clear all
    W = rand(1, 1000);
    res = my_sum(W)
end

function s = my_sum(V)
    s = 0;
    for v in V
        s = s + v;
    end
end

Funzioni e Script in Matlab pre-2016b

clear all è inutile (il record di attivazione è inizialmente vuoto)

function my_test()
    W = rand(1, 1000);
    res = my_sum(W)
end

function s = my_sum(V)
    s = 0;
    for v in V
        s = s + v;
    end
end

Inseriamo tutto questo in un file di funzione my_test.m

Funzioni e Script in Matlab pre-2016b

Per eseguire lo “script”, dobbiamo chiamarlo come funzione

…Del resto, a questo punto è una funzione

my_test() % esegue lo script

Nota: se vogliamo chiamare una funzione senza parametri:

• Matlab permette di omettere le parentesi “()”…
• …Quindi possiamo chiamare il nostro script/funzione anche con:

my_test

• Dà l’illusione di aver chiamato uno script
• In realtà, abbiamo chiamato una funzione (senza passarvi alcunché)

Un Esempio: Confronto di Orari

Problema: confrontare due orari

• HP: gli orari sono rappresentate come vettori di interi
• HP: nell’ordine, abbiamo [hh, mm]

Vogliamo definire nello script es_timecmp.m una funzione:

function res = timecmp(t1, t2)

Tale che il risultato sia

• -1 se il primo orario precede il secondo
• 0 se sono uguali
• +1 se il secondo orario precede il primo

Soluzione

Nel file di funzione es_timecmp.m:

function es_timecmp()
    res1 = timecmp([15, 00], [15, 21])
    res2 = timecmp([15, 00], [14, 59])
    res3 = timecmp([15, 00], [15, 00])
end

function res = timecmp(t1, t2)
  ...
end

• Vediamo una possibile definizione di timecmp…
• Non è efficiente, né elegante, ma è leggibile

Soluzione

Vediamo una possibile implementazione di timecmp:

function res = timecmp(t1, t2)
    res = 0;
    if t1(1) < t2(1)
        res = -1;
    end
    if t1(1) > t2(1)
        res = 1;
    end
    if t1(1) == t2(1) & t1(2) < t2(2)
        res = -1;
    end
    if t1(1) == t2(1) & t1(2) > t2(2)
        res = 1;
    end
end

Calore Molare

Il calore (specifico) molare di un sostanza:

• È il calore necessario per variare la temperatura di una mole di 1K
• Dipende dalla temperatura, secondo una legge polinomiale:

\[c_p^* = a + b\, T + c\, T^2 + d\, T^3\]

• Il polinomio è al più di 4° grado
• I coefficienti sono stati determinati empiricamente per varie sostanze

Avete visto/vedrete questi argomenti nel corso di Termodinamica

Polinomi in Matlab

Matlab fornisce funzioni per operare su polinomi

Un polinomio viene rappresentato come un vettore di coefficienti:

\[\underline{c_n} x^n + \underline{c_{n-1}} x^{n-1} + \ldots + \underline{c_1} x + \underline{c_0} \ \longleftrightarrow \ p = (c_n, c_{n-1}, \ldots c_1, c_0)\]

• Il primo elemento del vettore corrisponde a \(c_n\)
• L’ultimo elemento del vettore corrisponde a \(c_0\)
• Il grado del polinomio è dato da length(p)-1

Quindi, per il calore molare:

• Il polinomio \(a + b\, T + c\, T^2 + d\, T^3\)
• Viene rappresentato come: [d, c, b, a] (invertito!)

Esercizio

Consideriamo il composto \(n\)-ottano

Vogliamo studiarne il calore molare in funzione della temperatura

• I coefficienti A, B, C, D sono noti
• Vogliamo disegnare \(c_p^*\) in funzione di \(T\)…
• …Con \(T\) che va da 300K a 400K

Dobbiamo valutare un polinomio. In Matlab possiamo usare:

function X = polyval(P, X)

• P è il polinomio da valutare
• X è il valore di \(x\) e può essere anche un vettore
• Y è il vettore con la valutazione di ogni elemento di X

Esercizio

• Dal sito del corso, scaricate lo start-kit di questa lezione
• Iniziate a codificare dal file es_polyval.m nello start-kit

Parte 1: calcolate il calore molare con polyval di Matlab

• Effettuate il calcolo per \(T \in [300K, 400K]\)
• Disegnate la curva risultante con plot

Parte 2: nello stesso file, definite una funzione:

function y = my_polyval(p, x)

• Che calcoli il valore del polinomio p…
• …quando x è uno scalare (per semplicità)
• Calcolate una nuova curva con my_polyval e disegnatela

Differenza di Entalpia

Il valore di \(c_p^*\) è necessario per calcolare la differenza di Entalpia

\[\Delta H = \int_{T_0}^{T_1} c_p^*(T) \, dT\]

• L’entalpia è una misura di energia di un sistema termodinamico…
• …Ma questo penso lo sappiate meglio di me

Dal punto di vista matematico:

• Poiché \(c_p^*(T)\) è una funzione polinomiale…
• …La sua funzione integrale \(C_p^*(T)\) si può calcolare in modo simbolico

A partire da essa possiamo calcolare:

\[\Delta H = C_p^*(T_1) - C_p^*(T_0)\]

Integrazione e Derivazione di Polinomi

• Anche se possiamo calcolare l’integrale per via simbolica…
• …Non lo dobbiamo fare per forza con carta e penna!

Matlab fornisce una funzione per integrare e derivare polinomi

function P = polyint(p)

Dato un polinomio:

\[c_n\, x^n + c_{n-1}\, x^{n-1} + \ldots + c_1\, x + c_0\]

Il suo integrale è un altro polinomio, ossia:

\[\frac{1}{n+1} c_n\, x^{n+1} + \frac{1}{n} c_{n}\, x^{n-1} + \ldots + \frac{1}{2} c_1\, x^2 + c_0\, x\]

Integrazione e Derivazione di Polinomi

• Anche se possiamo calcolare l’integrale per via simbolica…
• …Non lo dobbiamo fare per forza con carta e penna!

Matlab fornisce una funzione per integrare e derivare polinomi

function P = polyint(p)

In termini della rappresentazione utilizzata da Matlab:

• p è il polinomio (vettore di coefficienti) da integrare
• P è il polinomio (vettore di coefficienti) risultato
• P ha un grado in più (un elemento in più) di p:

\[(c_n, c_{n-1}, \ldots c_1, c_0) \longrightarrow \left(\frac{1}{n+1} c_n, \frac{1}{n} c_{n-1}, \ldots \frac{1}{2} c_1, c_0, 0\right)\]

Integrazione e Derivazione di Polinomi

• Anche se possiamo calcolare l’integrale per via simbolica…
• …Non lo dobbiamo fare per forza con carta e penna!

Matlab fornisce una funzione per integrare e derivare polinomi

function P = polyint(p)

Per esempio:

polyint([1, 1, 1]) % denota [1/3, 1/2, 1, 0]
polyint([1, 2, 4]) % denota [1/3, 1, 4, 0]

• Attenzione: il risultato dell’integrazione è un polinomio…
• …Ci resta poi da valutarlo per i valori che ci interessano

Esercizio

Calcolate \(\Delta H\) per l’\(n\)-ottano tra 300K e 400K

Utilizzate come partenza il file es_polyint.m

Step 1: Calcolate il polinomio integrale \(C_p^*(T)\) con polyint

• Quindi usate polyval per calcolare \(C_p^*(T)\) a 300K e 400K
• Ottenete \(\Delta H\) per differenza

Step 2: Definite la funzione

function P = my_polyint(p)

• Che, dato un polinomio (vettore di coefficienti) p…
• …Calcoli il polinomio integrale P
• Confrontate il risultato con quello di polyint

Esercizio: Elementi Non Nulli

Matlab fornisce la funzione:

function I = find(X)

• che restituisce gli indici degli elementi diversi da 0

Nel file di script es_find , definite la funzione (ausiliaria):

function I = my_find(X)

• Che replichi tale funzionalità.

Scrivere del codice di test nella funzione principale

• Utilizzate un vettore definito a mano
• Infatti, rand non genera mai 0

Esercizio: Fattoriale di un Vettore

Matlab fornisce la funzione:

function F = factorial(V)

Che restituisce un vettore con il fattoriale di ogni numero in V

• Gli elementi di V devono essere numeri interi
• Il fattoriale \(n!\) di un numero \(n\) è definito come:

\[n! = \left\{\begin{aligned} & 1 && \text{ se } n = 0\\ & \prod_{i = 1}^n i && \text{ se } n > 0 \end{aligned}\right.\]

Esercizio: Fattoriale di un Vettore

Si definisca un file di funzione es_factorial, contenente:

Una funzione ausiliaria:

function F = my_factorial(V)

• Che replichi tale il comportamento di factorial

Si verifichi il funzionamento:

• Scrivendo le istruzioni di test nella funzione principale
• Si esegua my_factorial e factorial su un vettore scelto a mano
• Si confrontino i risultati

Esercizio: Indicizzazione con Valori Logici

Abbiamo visto che Matlab permette di accedere ad un vettore con:

V(I)

• V è un vettore
• I è un vettore di valori logici

Nel file di funzione es_index2.m, definite la funzione (ausiliaria):

function W = my_index2(V, I)

Che replichi la stessa funzionalità

• Verificate il funzionamento come al solito

Derivazione di Polinomi

In matematica, dato un polinomio:

\[c_n\, x^{n} + c_{n-1}\, x^{n-1} + \ldots + c_0\]

La sua derivata è un altro polinomio:

\[n\, c_n\, x^{n-1} + (n-1)c_{n-1}\, x^{n-2} + \ldots + c_1\]

In termini della rappresentazione utilizzata da Matlab:

\[(c_n, c_{n-1}, \ldots c_1, c_0) \longrightarrow (n c_n, (n-1) c_{n-1}, \ldots c_1)\]

• Derivando otteniamo un polinomio inferiore di un grado

Lo possiamo calcolare con la funzione predefinita:

function dp = polyder(p)

Esercizio

In un file di funzione es_polyder.m:

Definire una funzione (ausiliaria):

function dp = my_polyder(p)

• Che, dato un polinomio (vettore di coefficienti) p…
• …Calcolo il polinomio derivata dp

Quindi, nella funzione principale:

• Effettuate dei test con polinomi definiti a mano
• Confrontate i risultati con quelli di polyder

Esercizio: Elementi Distinti

Matlab fornisce la funzione:

function U = unique(X)

• X che restituisce gli elementi distinti del vettore X

Nel file di funzione es_unique.m, definite una la funzione (ausiliaria):

my_unique(X)

Che replichi la stessa funzionalità

• Matlab ordina anche il vettore di uscita: noi non lo faremo
• Verificate il funzionamento con un vettore costruito a mano