Esercizio: BMW-i8 (2)

Una BMW i8 accelera a tavoletta su un rettilineo

Esercizio: BMW-i8 (2)

Una BMW i8 accelera a tavoletta su un rettilineo

Supponiamo che il motore eroghi una forza costante $F$

• L’auto ha un motore elettrico, così l’assunzione non è così irrealistica

Si oppone alla direzione del moto la forza di trascinamento:

$$F_t = -\frac{1}{2} \rho C_D S v |v|$$

• $\rho$ è la densità dell’aria, $v$ è la velocità
• $S$ è la superficie della sezione dell’auto
• $C_D$ è un coefficiente di trascinamento

Esercizio: BMW-i8 (2)

Quindi il sistema è definito dall’ODE:

$$\ddot{x} = \frac{1}{m} (F + F_t)$$

• Dove $m$ è la massa dell’auto

L’andamento dello stato può essere determinato risolvendo l’ODE

Il codice per farlo è disponibile nel file es_bmw2.m

L’ODE viene risolta in una funzione:

function [t, x, v] = sim_bmw(tspan,x0,rho,A,C_D,M,F)

• Vedrete che sarà utile per svolgere l’esercizio

Esercizio: BMW-i8 (2)

Rispondete ai seguenti quesiti:

Q1: Determinare la velocità massima raggiunta in 60 sec

Q2: Si desidera migliorare l’aerodinamica dell’auto

• Determinare quale valore dovrebbe assumere $C_D$…
• …Perché la velocità massima del Q1 sia raggiunta in 30 sec.
• Suggerimento: definire e sfruttare una nuova funzione:

function tvmax = time_for_vmax(vmax, tspan, x0, ...)

• Che calcoli il tempo necessario a raggiungere vmax

Q3: Disegnare l’andamento della velocità per 60 sec…

• Con il vecchio ed il nuovo valore di $C_D$
• Si disegnino i due andamenti sulla stessa figura

Esercizio: Dalla Terra alla Luna (2)

Nel libro di Jule Verne “Dalle Terra alla Luna”…

• …Il veicolo con i protagonisti viene “sparato” verso la Luna

Esercizio: Dalla Terra alla Luna (2)

Durante il viaggio, la navicella è soggetta a forze gravitazionali

Esse sono regolate dalla legge di gravitazione di Newton:

$$F_{12} = -G \frac{m_1 m_2}{r_{12} |r_{12}|}$$

• $F_{12}$ è la forza esercitata dal corpo 2 sul corpo 1
• $G$ è la costante di gravitazione
• $m_1$ ed $m_2$ sono le masse del corpo 1 e 2
• $r_{12}$ è la distanza dal corpo 1 al corpo 2, i.e. $$r_{12} = x_1 - x_2$$
  • $x_1$ e $x_2$ sono le posizioni di 1 e 2
  • Funziona per scalari (la forma vettoriale è leggermente diversa)

Esercizio: Dalla Terra alla Luna (2)

Si desidera modellare il moto della navicella

• HP: Terra e Luna sono fisse $\Rightarrow$la traiettoria è verticale
• Il moto sarà regolato dell’equazione differenziale:

$$\ddot{x} = \frac{1}{m_s} (F_{se} + F_{sm})$$

• $m_s$ è la massa della navicella
• $F_{se}$ è l’attrazione esercitata dalla Terra sulla navicella
• $F_{sm}$ è l’attrazione esercitata dalla Luna sulla navicella
• HP: Il centro della Terra ha quota 0
• HP: La navicella parta da una quota $r_E$ (i.e. il raggio della Terra)
• La navicella deve raggiungere la quota $D-r_M$
• $D =$ distanza Terra-Luna, $r_M =$ raggio lunare

Il codice per risolvere l’ODE è nel file es_moonshot2.m

Esercizio: Dalla Terra alla Luna (2)

Si risponda ai seguenti quesiti:

Q1: Si determini la quota massima raggiunta dalla navicella

• Si controlli se sia superiore al valore $D - r_M$

Q2: Si determini la velocità iniziale della navicella…

• …Perché la quota $D - r_M$ sia raggiunta in esattamente 10 gg
• Allo scopo, si definisca e si sfrutti una funzione: j

function highest = find_highest(tspan, x0, ...) 

• Che determini la quota massima raggiunta nell’intervallo tspan

Q3: Si disegni l’andamento della posizione della navicella…

• …Con la vecchia e la nuova velocità iniziale (unica figura)

Esercizio: Riscaldamento di una Stanza (3)

Vogliamo riscaldare una stanza con un convettore

• Il convettore riscalda l’aria, che sua volta riscalda i muri
• …Che disperdono parte del calore verso l’esterno

Sappiamo che:

• La temperature del convettore e dell’esterno sono costanti
• L’aria della stanza ed i muri hanno capacità termiche non trascurabili

Possiamo modellare il sistema utilizzando un circuito RC equivalente:

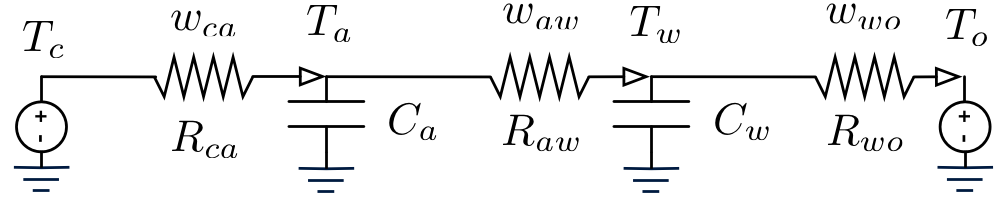
Esercizio: Riscaldamento di una Stanza (4)

Il sistema è definito dalle equazioni differenziali:

$$\begin{align} & \dot{T}_a = \frac{1}{C_a} (w_{ca} - w_{aw}) && \dot{T}_w = \frac{1}{C_w} (w_{aa} - w_{wo}) \\ \end{align}$$

Dove:

$$\begin{align} & w_{ca} = \frac{1}{R_{ca}} (T_c - T_a) \\ & w_{aw} = \frac{1}{R_{aw}} (T_a - T_w) \\ & w_{wo} = \frac{1}{R_{wo}} (T_w - T_o) \\ \end{align}$$

Il codice per risolvere la ODE è in es_heating3.m

Esercizio: Riscaldamento di una Stanza (4)

Si risponda ai seguenti quesiti:

Q1: si determini la temperature dell’aria dopo 1h

Q2: Si determini la temperature dal convettore…

• Perchè dopo 1h l’aria abbia raggiuno i 20.5°C
• SUGGERIMENTO: si definisca una funzione:

function  TA1h = find_TA1h(tspan, x0, ...)

• Che calcoli la temperatura dell’aria dopo 1h

Q3: Si disegnino i due andamenti di $T_a$

• Si utilizza una sola figura, per facilitare il confronto

Esercizio: Serbatoi Comunicanti (2)

Tre serbatoi comunicano attraverso condotte

Esercizio: Serbatoi Comunicanti (2)

Tre serbatoi comunicano attraverso condotte

• Il problema può essere modellato con un circuito RC
• Il modello è approssimativo, ma a noi basterà

Esercizio: Serbatoi Comunicanti (2)

Il sistema è descritto dalle equazioni differenziali:

$$\begin{align} & \dot{P}_1 = \frac{1}{C_1} (q_{31} - q_{12}) && \dot{P}_2 = \frac{1}{C_2} (q_{12} - q_{23}) \\ & \dot{P}_2 = \frac{1}{C_3} (q_{23} - q_{31}) \end{align}$$

Con:

$$\begin{align} & q_{12} = \frac{1}{R_{12}} (P_1 - P_2) && q_{23} = \frac{1}{R_{23}} (P_2 - P_3) \\ & q_{31} = \frac{1}{R_{31}} (P_3 - P_1) \end{align}$$

Il codice per risolvere la ODE è in es_tubes4.m

Esercizio: Serbatoi Comunicanti (2)

Si risponda ai seguenti quesiti:

Q1: Determinare la pressione $p^*$ del serbatoio 1 dopo 600 secondi

Q2: Determinare il valore di $R_{12}$ affinché…

• …La pressione del primo serbatoio valga $p^*$ dopo 400 secondi
• Allo scopo, si definisca e si sfrutti una funzione:

function p1_400 = find_p1_400(tspan, x0, ...)

• Che calcoli il valore di $P_1$ dopo 400 secondi

Q3: Si disegni l’andamento delle tre pressioni con il nuovo $R_{12}$

• Si utilizzi una nuova figura

Esercizio: Fiat 500

Una Fiat 500 in folle avanza su un rettilineo

Si vuole studiare il comportamento dell’auto in arresto

Esercizio: Fiat 500

Si oppone alla direzione del moto la forza di trascinamento:

$$F_t = -\frac{1}{2} \rho C_D S v |v|$$

• $\rho$ è la densità dell’aria, $v$ è la velocità
• $S$ è la superficie della sezione, $C_D$ è il coefficiente di trascinamento

L’auto è soggetta anche all’attrito volvente (rotolamento):

$$F_r = -C_R m g \tanh(4v)$$

• $m$ è la massa, $g$ l’accelerazione di gravità
• $C_R$ un coefficiente di attrito volvente
• $\tanh$ è la tangente iperbolica (tanh in Matlab)

Esercizio: Fiat 500

Quindi il sistema è definito dall’ODE:

$$\ddot{x} = \frac{1}{m} (F_r + F_t)$$

• L’andamento può essere determinato risolvendo l’ODE

I dati del problema sono definiti nel file es_fiat500.m

Q1: Si determini l’andamento di velocità e posizione fino all’arresto

• Si determini per tentativi un intervallo di tempo sufficiente lungo
• SUGGERIMENTO: incapsulare il codice in una funzione:

function [t,x,v] = sim_car(tspan,x0,g,rho,m,Cr,Cd,S)

• Si disegnino i due andamenti in due figure distinte

Esercizio: Fiat 500

Q2: Si determini il tempo necessario perché l’auto si fermi

• NOTA: nella nostra situazione, quando la velocità è nulla…
• …si annulla anche l’accelerazione

Q3: Si determini la strada percorsa fino all’arresto

Q4: Si determini la velocità iniziale perché l’auto si arresti dopo 300 m

• SUGGERIMENTO: si definisca una funzione

function xstop = find_xstop(tspan, x0, ...)

• Che determini dopo quanti metri avviene l’arresto