ODE e Sistemi Dinamici

Una equazione differenziale ordinaria (ODE) è definita da:

$$\dot{x} = f(t, x)$$

• Dove $t$ è una variabile scalare
• $x$ è una funzione di $t$, potenzialmente con valori vettoriali, i.e.:

$$x : \mathbb{R} \mapsto \mathbb{R}^n$$

• $\dot{x}$ è la derivata di $x$ in $t$

Informalmente, una eq. diff. ord. definisce un sistema dinamico

• $x$ è lo stato del sistema, che evolve nel tempo $t$
• $f$ specifica come la derivata di $x$ dipenda dallo stato e dal tempo
• Il tempo è una variabile continua $\Rightarrow$ il sistema è tempo-continuo

Riduzione al Primo Ordine

È sufficiente limitarsi alla derivata del primo ordine

• Se ci sono derivate di ordine maggiore, e.g. $\ddot{x}$…
• …Possono essere sempre ricondotte al primo ordine…
• …Introducendo un elemento di stato per ogni derivata intermedia

Per esempio:

$$\ddot{x} = a t^2$$

Introducendo $y = \dot{x}$, diventa:

$$\left(\begin{array}{c} \dot{x} \\ \dot{y} \end{array}\right) = \left(\begin{array}{c} y \\ a t^2 \end{array}\right)$$

• Caso tipico: $x =$ posizione, $y =$ velocità

Problemi ai Valori Iniziali

Quando si risolve una ODE, l’obiettivo è determinare $x$

Ma $x$ è una funzione! Quindi vogliamo determinarne l’andamento

• Per farlo, è necessario fare alcune assunzioni addizionali…
• …Per esempio, possiamo specificare un valore iniziale

In questo modo otteniamo un problema ai valori inziali:

$$\begin{align} & \dot{x} = f(t, x) \\ & x(0) = x_0 \end{align}$$

Intuitivamente, si tratta di simulare il sistema dinamico

• Poiché il sistema è tempo-continuo, $f$ non determina lo stato futuro…
• …Ma il modo in cui lo stato varia (i.e. la sua derivata)

ODE in Matlab

Matlab mette a disposizione diversi risolutori di ODE

Quello che utilizzeremo principalmente è accessibile mediante:

function [T, X] = ode45(f, tspan, x0)

Per quanto riguarda i parametri di ingresso/uscita:

• f è la funzione che definisce la ODE. La sua interfaccia deve essere:

function dx = f(t, x)

• t è il “tempo”
• x è lo stato corrente (un vettore)
• dx è la derivata dello stato corrente (un vettore colonna)

ODE in Matlab

Matlab mette a disposizione diversi risolutori di ODE

Quello che utilizzeremo principalmente è accessibile mediante:

function [T, X] = ode45(f, tspan, x0)

Per quanto riguarda i parametri di ingresso/uscita:

• tspan è un vettore con i due estremi dell’intervallo di simulazione
  • E.g. tspan = [0, 3600]
• x0 è lo stato iniziale
• T contiene tutti gli istanti di tempo visitati dall’algoritmo
• Ogni riga della matrice X contiene uno stato visitato
  • Esattamente come per la nostra vecchia simulate

Esempio: L’Auguste Piccard PX-8

L’attrattiva principale dell’Expo 1964 fu un sottomarino

• Faceva immersioni con passeggeri nel Lago di Ginevra

Esempio: L’Auguste Piccard PX-8

Per muoversi in verticale un sottomarino carica/scarica acqua

In questo modo esso varia la sua densità

• Se la densità è maggiore di $\rho$, il sottomarino “cade” nel fluido
• Se è minore, il sottomarino “cade” verso l’alto
• Se è uguale, il sottomarino si muove per inerzia

Per precisione, il sottomarino è soggetto a tre forze principali:

• La forza di gravità, che lo accelera verso il basso
• La forza di galleggiamento, che lo accelera verso l’alto
• L’attrito aerodinamico dell’acqua (trascinamento)

Esempio: L’Auguste Piccard PX-8

Sia $L$ il volume dell’acqua a bordo, allora abbiamo che:

La forza di gravità è data da (asse cartesiano orientato verso l’alto):

$$F_g = -g (m + \rho L)$$

• $m$ è la massa del sottomarino
• $g$ è l’accelerazione di gravità
• $\rho$ è la densità dell’acqua

La forza di galleggiamento è data da (principio di Archimede):

$$F_b = g \rho V$$

• $V$ è il volume del sottomarino

Esempio: L’Auguste Piccard PX-8

Sia $L$ il volume dell’acqua a bordo, allora abbiamo che:

• L’attrito aerodinamico dell’acqua (trascinamento) è dato da:

$$F_t = -\frac{1}{2} \rho A C_D\, v |v|$$

• $A$ è l’area della sezione
• $C_D$ è un coefficiente che dipende dalla forma
• $v$ è la velocità
  • Il prodotto $v |v|$ ha lo stesso segno di $v$…
  • …ed il valore assoluto di $v^2$

Esempio: L’Auguste Piccard PX-8

Supponiamo che l’acqua a bordo vari nel modo seguente:

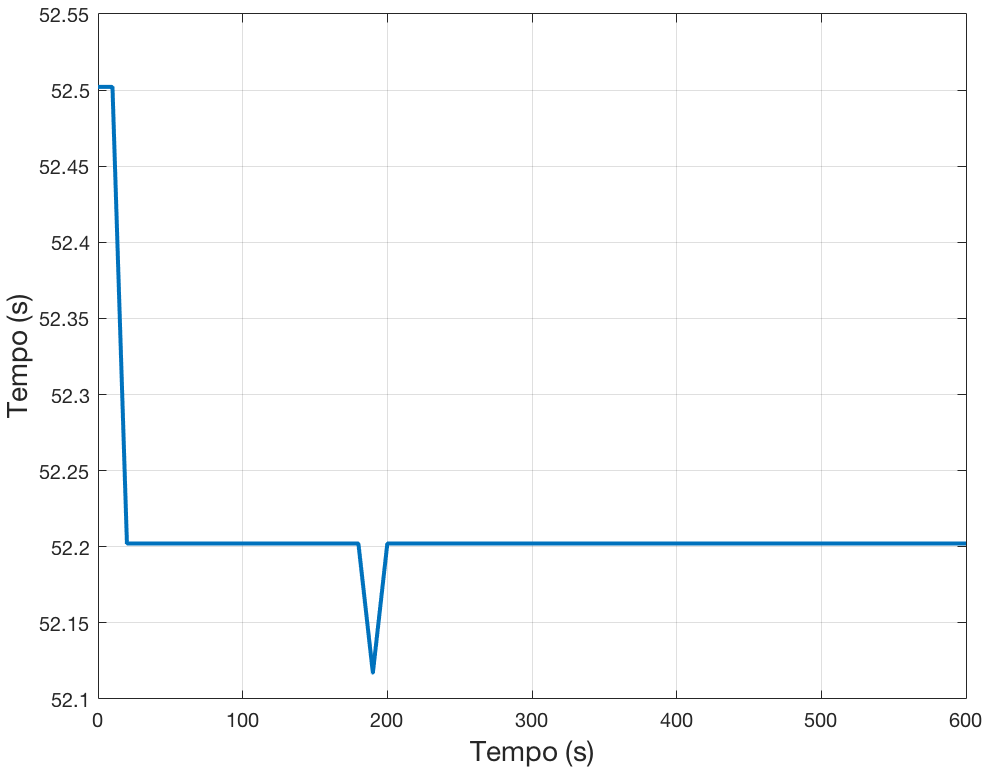
• Il valore $L \simeq 52.2$ bilancia le forze di gravità e galleggiamento

Esempio: L’Auguste Piccard PX-8

In pratica, $L$ varia secondo una funzione lineare a tratti

• In Matlab la si può valutare con interp1
• I punti Tp e Lp che definiscono la funzione sono in es_submarine.m
• Il file contiene anche tutte le informazioni sul PX-8

Si desidera calcolare la quota del PX-8 nel tempo

• Questa è regolata dall’equazione differenziale:

$$\ddot{x} = \frac{1}{m + \rho L} (F_g + F_b + F_t)$$

• La quota iniziale $x_0$ è $-5\, m$
• In particolare, quale è la quota dopo 10, 20 e 30 minuti?

Esempio: L’Auguste Piccard PX-8

Dobbiamo risolvere un problema ai valori iniziali

Per farlo, dovremo invocare:

function [T, X] = ode45(f, tspan, x0)

Quindi dobbiamo determinare:

• Come descrivere lo stato $X$ del sistema
  • Una buona scelta: $X = (\text{posizione}, \text{velocità})$
• L’intervallo di simulazione
  • Una buona scelta: $[0, 1800]$ (30 minuti)
• La funzione f che ne calcola la derivata

Esempio: L’Auguste Piccard PX-8

Per definire f è utile procedere nel solito modo:

• Prima definiamo una funzione che calcoli la derivata dello stato…
• …A partire da tutti i dati del problema

function dx = dstate(t,x,g,V,M,rhoW,Cd,S,Tp,Lp)
    % x(1) = altitudine, x(2) = velocita'
    Fb = g * rhoW * V; % Galleggiamento
    L = interp1(Tp, Lp, t); % Carico d'acqua
    Fg = -(g*M + g*rhoW * L); % Gravità
    Ft = -0.5 * x(2) * abs(x(2)) * Cd * S * rhoW;
    % Calcolo le derivate
    dx(1) = x(2);
    dx(2) = (Fb+Fg+Ft) / (M + rhoW * L);
end

Esempio: L’Auguste Piccard PX-8

Per definire f è utile procedere nel solito modo:

• Quindi definiamo una funzione anonima…
• …Che esponga solo due parametri (i.e. $t$ ed $X$)

La funzione anonima potrà essere utilizzata per invocare ode45

dX = @(t, x) dstate(t,x,g,V,M,rhoW,Cd,S,Tp,Lp)';
x0 = [-5, 0]; % Stato iniziale
tspan = [0, 1800];
[t, X] = ode45(dX, tspan, x0);

• Notate che dX deve restituire un vettore colonna…
• …Per questa ragione trasponiamo il risultato di dstate
• Ricordate che la quota iniziale è $-5\, m$

Esempio: L’Auguste Piccard PX-8

A questo punto possiamo recuperare quota e velocità

x = X(:, 1); % Quota (prima colonna)
v = X(:, 2); % Velocità (seconda colonna)

Possiamo disegnare l’andamento della quota:

plot(t, x)

Esempio: L’Auguste Piccard PX-8

A questo punto possiamo recuperare quota e velocità

x = X(:, 1); % Quota (prima colonna)
v = X(:, 2); % Velocità (seconda colonna)

Ed ottenere la quota dopo 10, 20, 30 minuti:

x10 = interp1(t, x, 10 * 60)
x20 = interp1(t, x, 20 * 60)
x30 = interp1(t, x, 30 * 60)

• Usiamo interp1 perché la “funzione quota” x è definita per punti

Esercizio: BMW-i8

Una BMW i8 accelera a tavoletta su un rettilineo

Esercizio: BMW-i8

Una BMW i8 accelera a tavoletta su un rettilineo

Supponiamo che il motore eroghi una forza costante $F$

• L’auto ha un motore elettrico, così l’assunzione non è così irrealistica

Si oppone alla direzione del moto la forza di trascinamento:

$$F_t = -\frac{1}{2} \rho C_D S v |v|$$

• $\rho$ è la densità dell’aria, $v$ è la velocità
• $S$ è la superficie della sezione dell’auto
• $C_D$ è un coefficiente di trascinamento

Esercizio: BMW-i8

Quindi il sistema è definito dall’ODE:

$$\ddot{x} = \frac{1}{m} (F + F_t)$$

• Dove $m$ è la massa dell’auto

Tutti i dati sono nel file es_bmw.m

• Si determini l’andamento di velocità e posizione per 60 sec
• Si disegni l’andamento della velocità
• Si determini il tempo necessario per raggiungere i 27.8 m/s
• Si determini la strada percorsa in tale tempo
• Si determini la massima velocità raggiunta

Esercizio: Riscaldamento di una Stanza (2)

Vogliamo riscaldare una stanza con un convettore

• Il convettore riscalda l’aria, che sua volta riscalda i muri
• …Che disperdono parte del calore verso l’esterno
• La temperature del convettore e dell’esterno sono costanti
• L’aria della stanza ed i muri hanno capacità termiche non trascurabili

Possiamo modellare il sistema utilizzando un circuito RC equivalente:

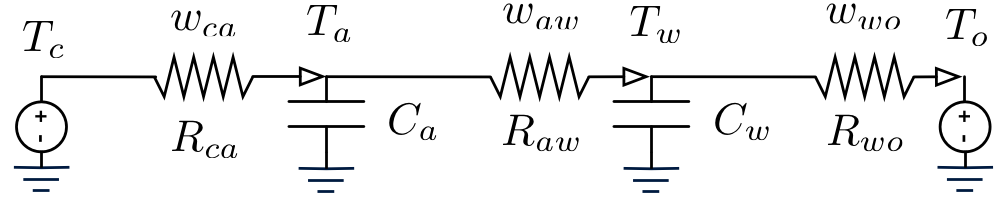
• Cerchi = generatori di tensione (temperature)
• Zig-zag = resistenze (resistenze termiche)
• Linee parallele = capacitori (capacità termiche)

Esercizio: Riscaldamento di una Stanza (2)

Vogliamo ottenere un modello tempo-continuo

Ogni capacità si può modellare con una equazione differenziale:

$$\begin{align} & \dot{T}_a = \frac{1}{C_a} (w_{ca} - w_{aw}) && \dot{T}_w = \frac{1}{C_w} (w_{aw} - w_{wo}) \end{align}$$

Esercizio: Riscaldamento di una Stanza (2)

Vogliamo ottenere un modello tempo-continuo

I flussi invece si calcolano mediante equazioni lineari:

$$\begin{align} & w_{ca} = \frac{1}{R_{ca}} (T_c - T_a) \\ & w_{aw} = \frac{1}{R_{aw}} (T_a - T_w) \\ & w_{wo} = \frac{1}{R_{wo}} (T_w - T_o) \\ \end{align}$$

Esercizio: Riscaldamento di una Stanza (2)

Quindi nel complesso abbiamo le equazioni differenziali:

$$\begin{align} & \dot{T}_a = \frac{1}{C_a} (w_{ca} - w_{aw}) && \dot{T}_w = \frac{1}{C_w} (w_{aw} - w_{wo}) \\ \end{align}$$

Dove:

$$\begin{align} & w_{ca} = \frac{1}{R_{ca}} (T_c - T_a) \\ & w_{aw} = \frac{1}{R_{aw}} (T_a - T_w) \\ & w_{wo} = \frac{1}{R_{wo}} (T_w - T_o) \\ \end{align}$$

Esercizio: Riscaldamento di una Stanza (2)

Tutti dati del problema sono disponibile ne file es_heating2.m

• Assumendo che i valori iniziali di $T_a$ e $T_w$ siano noti…
• …vogliamo determinare l’andamento delle temperature per 2 ore
• Si disegni su un unico grafico l’andamento di $T_a$ e $T_w$
• Si determini la temperatura finale dell’aria e dei muri
• Si determini la temperature dell’aria e dei muri dopo un’ora
• Si determini il tempo necessario perché l’aria raggiunga i 20°C

Esercizio: Dalla Terra alla Luna

Nel libro di Jule Verne “Dalle Terra alla Luna”…

• …Il veicolo con i protagonisti viene “sparato” verso la Luna

Esercizio: Dalla Terra alla Luna

Durante il viaggio, la navicella è soggetta a forze gravitazionali

Esse sono regolate dalla legge di gravitazione di Newton:

$$F_{12} = -G \frac{m_1 m_2}{r_{12} \|r_{12}\|}$$

• $F_{12}$ è la forza esercitata dal corpo 2 sul corpo 1
• $G$ è la costante di gravitazione
• $m_1$ ed $m_2$ sono le masse del corpo 1 e 2
• $r_{12}$ è la distanza dal corpo 1 al corpo 2, i.e. $$r_{12} = x_1 - x_2$$
  • $x_1$ e $x_2$ sono le posizioni di 1 e 2
  • Funziona per scalari (la forma vettoriale è leggermente diversa)

Esercizio: Dalla Terra alla Luna

Si desidera modellare il moto della navicella

• Assumiamo per semplicità che la Terra e la Luna siano in fisse
• Quindi la nave viaggerà lungo una traiettoria verticale
• Il moto sarà regolato dell’equazione differenziale:

$$\ddot{x} = \frac{1}{m_s} (F_{se} + F_{sm})$$

• $m_s$ è la massa della navicella
• $F_{se}$ è l’attrazione esercitata dalla Terra sulla navicella
• $F_{sm}$ è l’attrazione esercitata dalla Luna sulla navicella

Esercizio: Dalla Terra alla Luna

Inoltre, assumiamo che:

• Il centro della Terra abbia quota 0
• La navicella parta da una quota $r_E$ (i.e. il raggio della Terra)

La navicella deve così raggiungere la quota $D-r_M$

• Con $D =$ distanza Terra-Luna e $r_M =$ raggio lunare

I dati del problema sono nel file es_moonshot.m

• Si disegni l’andamento della quota della navicella
  • Come velocità iniziale, si usino sia $11,000\, m/s$ che $11,100\, m/s$
  • Si verificano problemi di calcolo? Perché?
• Si determini la quota massima raggiunta: è superiore a $D-r_M$?

Esercizio: Serbatoi Comunicanti

Tre serbatoi comunicano attraverso condotte

Esercizio: Serbatoi Comunicanti

Tre serbatoi comunicano attraverso condotte

• Il problema può essere modellato con un circuito RC
• Serbatoi = capacitori, resistenze = condotte
• Flussi = correnti, Differenza di pressione = differenza di tensione
• Il modello è approssimativo, ma a noi basterà

Esercizio: Serbatoi Comunicanti

Il sistema è descritto dalle equazioni differenziali:

$$\begin{align} & \dot{P}_1 = \frac{1}{C_1} (q_{31} - q_{12}) && \dot{P}_2 = \frac{1}{C_2} (q_{12} - q_{23}) \\ & \dot{P}_2 = \frac{1}{C_3} (q_{23} - q_{31}) \end{align}$$

Con:

$$\begin{align} & q_{12} = \frac{1}{R_{12}} (P_1 - P_2) && q_{23} = \frac{1}{R_{23}} (P_2 - P_3) \\ & q_{31} = \frac{1}{R_{31}} (P_3 - P_1) \end{align}$$

Esercizio: Serbatoi Comunicanti

Tutti i dati del problema sono nel file es_tubes.m

• Assumendo che tutte le pressioni iniziali siano note…
• …Si determini e disegni l’andamento delle tre pressioni nel tempo
• Si determini la pressione nel serbatoio 1 dopo 600 minuti
• Dopo quanto tempo la differenza tra $P_1$ e $P_2$ è minore di $10^{-1}$?