Esempio: Argine di un Fiume

Supponiamo di dover progettare l’argine di un fiume

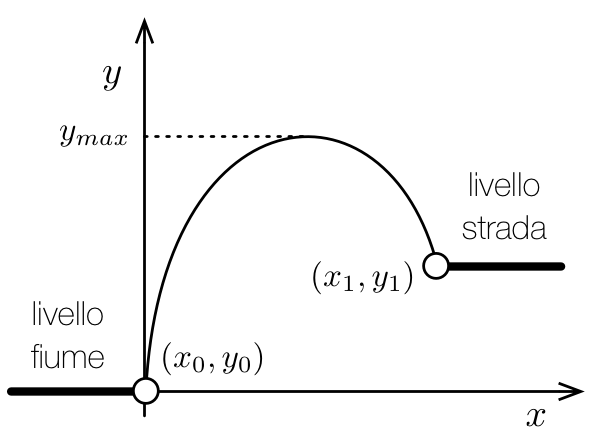
• Alle ascisse abbiamo una posizione orizzontale \(x\)
• Alle ordinate abbiamo l’altezza \(y\)

Esempio: Argine di un Fiume

L’argine deve:

• Essere definito da una curva parabolica
• Toccare il fiume in una posizione nota \((x_0, y_0)\)
• Raggiungere il livello della strada nel punto \((x_1, y_1)\)
• Raggiungere l’altezza massima \(y_{max}\)…
• In un punto di coordinata \(x_2\) non nota

Di fatto, si tratta di progettare/tracciare una curva

• Allora possiamo provare a risolverlo…
• …Impostando un insieme di equazioni

Equazioni per il Problema

Proviamo a formulare equazioni per le condizioni da rispettare:

• La curva deve passare per il punto \((x_0, y_0)\):

\[\alpha_2 x_0^2 + \alpha_1 x_0 + \alpha_0 = y_0\]

• La curva deve passare per il punto \((x_1, y_1)\):

\[\alpha_2 x_1^2 + \alpha_1 x_1 + \alpha_0 = y_1\]

• La curva raggiungerà il max nel punto \(x_2\) in cui la derivata si annulla:

\[2 \alpha_2 x_2 + \alpha_1 = 0\]

• In corrispondenza di \(x_2\), l’altezza dovrà essere \(y_{max}\):

\[\alpha_2 x_2^2 + \alpha_1 x_2 + \alpha_0 = y_{max}\]

Equazioni per il Problema

Nel complesso, abbiamo:

\[\begin{align} \alpha_2 x_0^2 + \alpha_1 x_0 + \alpha_0 &= y_0 \\ \alpha_2 x_1^2 + \alpha_1 x_1 + \alpha_0 &= y_1 \\ 2 \alpha_2 x_2 + \alpha_1 &= 0 \\ \alpha_2 x_2^2 + \alpha_1 x_2 + \alpha_0 &= y_{max} \end{align}\]

• Le variabili sono \(\alpha_2, \alpha_1, \alpha_0\), ma anche \(x_2\)
• Ci sono delle espressioni non lineari, i.e. \(\alpha_2 x_2, \alpha_2 x_2^2, \alpha_1 x_2\)

In sostanza, abbiamo un sistema di equazioni non lineari:

• Quindi, non possiamo impostare il problema in forma matriciale!

Equazioni Non Lineari in Matlab

Per risolvere equazioni non lineari Matlab offre due funzioni:

function [X, FVAL, FLAG] = fzero(F, X0)
function [X, FVAL, FLAG] = fsolve(F, X0)

Entrambe risolvono equazioni nella forma:

\[f(x) = 0\]

• In altre parole, cercano di trovare un valore di \(x\)…
• …Che azzeri la funzione \(f(x)\)
• Procedono in moto iterativo
• Una di esse (fsolve) potrebbe non convergere

Una soluzione dell’equazione è detta uno zero della funzione

Equazioni Non Lineari in Matlab

Per risolvere equazioni non lineari Matlab offre due funzioni:

function [X, FVAL, FLAG] = fzero(F, X0)
function [X, FVAL, FLAG] = fsolve(F, X0)

Per quanto riguarda i parametri, abbiamo che:

• X0 è la stima iniziale di \(x\) da cui partire
• F è la funzione da azzerare (passata come parametro)
• F deve avere un singolo parametro, i.e.:

function z = F(X)

• Il parametro (i.e X) corrisponde alla variabile \(x\)

Equazioni Non Lineari in Matlab

Per risolvere equazioni non lineari Matlab offre due funzioni:

function [X, FVAL, FLAG] = fzero(F, X0)
function [X, FVAL, FLAG] = fsolve(F, X0)

Per quanto riguarda i valori restituiti abbiamo che:

• X è l’ultimo valore di \(x\) visitato
  • Se tutto è andato bene, è la soluzione
• FVAL è il valore di F in corrispondenza di X
  • Se tutto è andato bene, sarà molto vicino a 0
• FLAG è un numero che indica come sono andate le cose
  • Se vale 1, l’algoritmo ha trovato uno zero
  • Altrimenti, qualcosa è andato storto (consultate help)

Equazioni Non Lineari in Matlab

Per risolvere equazioni non lineari Matlab offre due funzioni:

function [X, FVAL, FLAG] = fzero(F, X0)
function [X, FVAL, FLAG] = fsolve(F, X0)

Le due funzioni usano una combinazione di metodi numerici

• fzero è basata (grossomodo) sul metodo della bisezione
  • Cerca di trovare un secondo punto x1…
  • …Tale che F(X0) e F(X1) abbiamo segni opposti
  • Se ce la fa e se F è continua, allora converge sempre
• fsolve usa metodi completamente diversi (i.e. trust region)
  • Non è garantito che converga…
  • …Ma può essere più veloce di fzero

Equazioni Non Lineari in Matlab

Per risolvere equazioni non lineari Matlab offre due funzioni:

function [X, FVAL, FLAG] = fzero(F, X0)
function [X, FVAL, FLAG] = fsolve(F, X0)

Il valore di x0 è molto importante:

• Se è scelto male, può impedire la convergenza
  • Nel caso di fzero, perché non si riesce a trovare un x1 adeguato
  • Nel caso di fsolve, per i limiti del metodo stesso
• Se ci sono più soluzioni, può determinare quale sia restituita
  • Il più delle volte, sarà la soluzione più vicina ad x0…
  • …Ma in generale non è garantito

Di solito, il valore di x0 si sceglie per intuizione o per tentativi

Sistemi di Equazioni Non Lineari

Per risolvere un sistema di equazioni non lineari…

…Cerchiamo lo zero di una funzione vettoriale, ossia risolviamo:

\[\begin{align} & F(x) = 0 && \text{con } F: \mathbb{R}^n \mapsto \mathbb{R}^m \end{align}\]

• Dove \(n\) ed \(m\) sono il numero di variabili e di equazioni.

Per esempio:

\[\begin{align} x^3 &= e^y \\ \log x &= y+1 \end{align} \longleftrightarrow F((x,y)) = (0, 0)\]

• Con:

\[F((x,y)) = \left(\begin{array}{cc} x^3 - e^y, & \log x - y-1 \end{array}\right)\]

Sistemi di Equazioni Non Lineari

Per i sistemi di equazioni non lineari…

…Possiamo usare solo fsolve

function [X, FVAL, FLAG] = fsolve(F, X0)

In questo caso:

• La funzione F dovrà avere ancora un singolo parametro:

function Z = F(X)

• Questa volta, però, X sarà un vettore anziché uno scalare
• E lo stesso vale per il valore di ritorno Z

fsolve cercherà un vettore X per cui F(X) restituisca un vettore nullo

Argine di un Fiume: Equazioni

Torniamo al nostro problema

• Innanzitutto portiamo tutti i membri a sx del segno =:

\[\begin{align} \alpha_2 x_0^2 + \alpha_1 x_0 + \alpha_0 - y_0 &= 0\\ \alpha_2 x_1^2 + \alpha_1 x_1 + \alpha_0 - y_1 &= 0\\ 2 \alpha_2 x_2 + \alpha_1 &= 0\\ \alpha_2 x_2^2 + \alpha_1 x_2 + \alpha_0 - y_{max} &= 0 \end{align}\]

Le espressioni definiscono i termini di una funzione vettoriale:

• La funzione dovrà avere come input un singolo vettore (e.g. “\(\bf x\)”)
• Il vettore dovrà contenere tutte le variabili:

\[{\bf x} = (\alpha_2, \alpha_1, \alpha_0, x_2)\]

• L’ordine può (come sempre) essere scelto liberamente

Argine di un Fiume: Implementazione

A questo punto possiamo codificare la funzione in Matlab:

function z = f(a2, a1, a0, x0, x1, y0, y1, x2, ymax)
    % La curva deve passare per (x0, y0)
    z(1) = a2*x0^2 + a1*x0 + a0 - y0;
    % La curva deve passare per (x1, y1)
    z(2) = a2*x1^2 + a1*x1 + a0 - y1;
    % La derivata si deve annullare in X(4)
    z(3) = 2*a2*x2 + a1;
    % in X(4) la curva deve valere ymax
    z(4) = a2*x2^2 + a1*x2 + a0 - ymax;
end

• La variabile restituita z è un vettore di 4 elementi

Argine di un Fiume: Implementazione

La nostra f è la funzione da azzerare

• Ma ha troppi argomenti!
• fsolve richiede una funzione con un singolo argomento

Risolviamo il problema con una funzione anonima:

x0 = 0;
x1 = 7;
y0 = 0;
y1 = 2;
ymax = 5;
% Espongo un solo parametro
fz = @(X) f(X(1),X(2),X(3),x0,x1,y0,y1,X(4),ymax);

• Il parametro da esporre è X, il vettore delle variabili

Implementazione

Per trovare uno zero a questo punto usiamo:

[psol, fval, flag] = fsolve(fz, x0)

• In questo caso x0 specificherà un valore per ogni variabile
• Per esempio, potremmo avere: x0 = [-1, 1, 0, 3]

Scegliere il valore \(x_0\) per i sistemi di equazioni può essere complicato

• Ci sono molti valori da decidere…
• …E disegnare la funzione può essere complicato (troppe dimensioni)

Come linea guida:

• Usate l’intuizione! Specie se il problema ha senso fisico
• Se qualcosa non torna, fate diversi tentativi

Soluzione

Per il nostro problema, l’argine avrà questa forma:

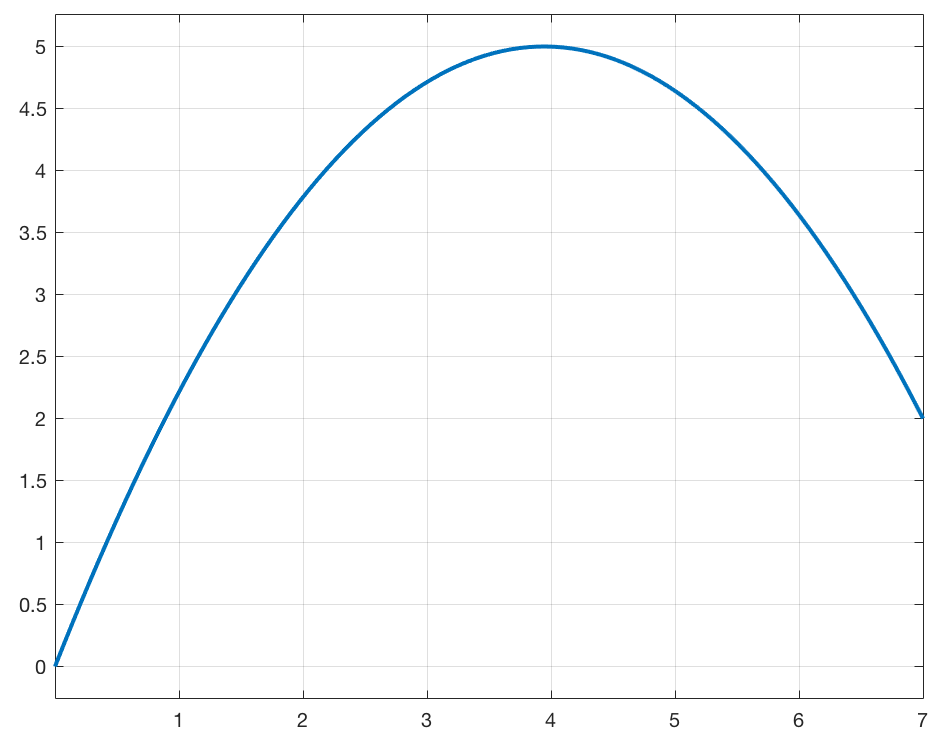
• Il massimo è raggiunto per \(x_2 = 3.9446\)

Esercizio: Argine di un Fiume (2)

Consideriamo di nuovo l’esempio di costruzione di un argine

Come in precedenza:

• Alle ascisse abbiamo una posizione orizzontale \(x\)
• Alle ordinate abbiamo l’altezza \(y\)

Esercizio: Argine di un Fiume (2)

L’argine deve:

• Essere definito da una curva parabolica \(f\)
• Toccare il fiume in una posizione nota \((x_0, y_0)\)
• Toccare la strada in un punto \((x_1, y_1)\)…
• …Di cui non è nota la coordinata \(x_1\)
• Raggiungere l’altezza massima \(y_{max}\)
• Avere una superficie complessiva pari a \(s\)

La superficie sarà data da:

\[S = \int_{\underbrace{x_0}_{= 0}}^{x_1} f(x) \, dx\]

Esercizio: Argine di un Fiume (2)

Il file es_riverbank2.m contiene i dati del problema:

• Impostate il problema di definizione della curva…
• …Vedrete che otterrete un sistema non lineare
• Risolvetelo con gli strumenti messi a disposizione da Matlab…
• …Dopo aver introdotto una o più funzioni opportunamente definite
• Disegnate l’andamento della curva dell’argine

Suggerimento:

• Usate una funzione “normale” per definire le equazioni…
• …Ed una funzione anonima per esporre solo i parametri desiderati
• Non è obbligatorio farlo, ma verrà comodo in futuro

Esercizio: Equilibri per Shepherd

Si consideri il modello di Shepherd:

\[x^{(k+1)} = \frac{r x^{(k)}}{1 + \left(\frac{x^{(k)}}{N}\right)^2 }\]

È un modello tempo-discreto per l’evoluzione di una popolazione:

• \(x^{(k)}\) è il numero di individui al passo \(k\)-mo
• \(r\) è un tasso di crescita
• \(N\) è il valore di popolazione per il cui \(r\) dimezza

Esercizio: Equilibri per Shepherd

Si consideri il modello di Shepherd:

\[x^{(k+1)} = \frac{r x^{(k)}}{1 + \left(\frac{x^{(k)}}{N}\right)^2 }\]

Il file es_shepherd.m nello start-kit contiene un simulatore

• Vogliamo provare a determinare lo stato di equilibrio…
• …Risolvendo l’equazione non lineare:

\[x = \frac{r x}{1 + \left(\frac{x}{N}\right)^2 }\]

• In pratica, richiediamo che lo stato non vari (i.e \(x^{(k+1)} = x^{(k)}\))

Esercizio: Equilibri per Shepherd

Estendete il codice in es_shepherd.m

Costruite opportunamente la funzione da azzerare

• Disegnate l’andamento della funzione da azzerare
• …Così da individuare visivamente la posizione degli zeri

Trovate lo zero con fzero o fsolve

• Verificate anche i valori restituiti di fval e flag

Provate a variare il valore di partenza \(x_0\)

• Cercate di ottenere due punti di equilibrio diversi

Esercizio: Equilibri per Crescita Logistica

Si consideri il modello di Crescita Logistica:

\[x^{(k+1)} = r x^{(k)} \left(1 - \frac{x^{(k)}}{N}\right)\]

Che può essere utilizzato per l’evoluzione di una popolazione

• \(x^{(k)}\) è il numero individui al passo \(k\)-mo
• \(r\) è un tasso di crescita
• \(N\) è il massimo valore della popolazione sostenibile

Il file es_logi_eq.m nello start-kit contiene un simulatore

• Vogliamo provare a determinare lo stato di equilibrio…
• …Risolvendo una equazione non lineare

Esercizio: Equilibri per Crescita Logistica

Estendete il codice in es_logi_eq.m

Costruite opportunamente la funzione da azzerare

• Disegnate l’andamento della funzione da azzerare…
• …Così da individuare visivamente la posizione degli zeri

Trovate lo zero con fzero o fsolve

• Verificate anche i valori restituiti di fval e flag

Provate a variare il valore di partenza \(x_0\)

• Osservate se viene trovato uno zero diverso

Esercizio: Crescita Logistica, Preda-Predatore

Si consideri questo modello preda-predatore visto a lezione:

\[\begin{align} & H^{(t+1)} = \overbrace{r \left(1 - \frac{H^{(t)}}{k} \right) H^{(t)}}^{\text{crescita logistica}} - \overbrace{s\, H^{(t)} P^{(t)}}^{\text{prede eliminate}} \\ & P^{(t+1)} = \underbrace{u\, P^{(t)}}_{\text{calo in assenza di prede}} + v \underbrace{\left( s\, H^{(t)} P^{(t)} \right)}_{\text{prede eliminate}} \end{align}\]

• \(H\) è il numero di prede e \(P\) quello di predatori
• \(k\) è la massima popolazione di prede sostenibile
• \(s\) è la frazione di \(H^{(t)}\) che un predatore può “mangiare”
• \(u < 1\) è il ritmo di scomparsa dei predatori in assenza di prede
• \(v\) è il “bonus riproduttivo” per ogni preda “mangiata”

Esercizio: Crescita Logistica, Preda-Predatore

Il file es_logi_pp_eq.m contiene un simulatore:

• Si estenda il codice così da determinare un punto di equilibrio…
• …Risolvendo un sistema di equazioni non lineari

Il punto di partenza \(x_0\) sarà in questo caso un vettore:

• Conterrà il numero iniziale di prede e predatori
• Per tentativi, trovate un \(x_0\) tale che la soluzione trovata…
• …coincida con lo stato stabile raggiunto dalla simulazione

Esercizio: Gas Isoentropico

In un fluido comprimibile isoentropico all’equilibrio…

…Pressione e temperature si distribuiscono secondo le equazioni:

\[\begin{align} & p = p_0 \left[ 1 + \left(1 - \frac{1}{\gamma}\right) \frac{M}{R T_0} g (z_0 - z) \right]^{\frac{\gamma}{\gamma - 1} } \\ & T = T_0 \left[ 1 + \left(1 - \frac{1}{\gamma}\right) \frac{M}{R T_0} g (z_0 - z) \right] \end{align}\]

• \(P, T\) sono la pressione e temperatura a quota \(z\)
• \(P_0, T_0\) sono la pressione e temperatura a quota \(z_0\)
• \(R\) è la costante dei gas perfetti
• \(M\) è la massa del gas
• \(\gamma\) è un parametro che caratterizza il gas

Esercizio: Gas Isoentropico

Se sono noti \(P_0, T_0, \gamma, M, z_0-z\), determinare \(P\) e \(T\) è facile:

• Perché le due equazioni sono esplicite in \(P\) e \(T\)
• Vale a dire: \(P\) e \(T\) compaiono da sole a sx dell’uguale

Supponiamo invece di disporre di \(P, T, P_0, T_0\) e \(z_0 - z\)

• A partire dai dati noti (e.g. misurati con qualche strumento)…
• …Vogliamo determinare le caratteristiche del gas (i.e \(\gamma\) e \(M\))
• Le due equazioni date sono implicite in \(\gamma\) e \(M\)…
• …Perché \(\gamma\) e \(M\) non possono essere isolate a sx del segno “=”

Quindi dobbiamo risolvere un sistema di due equazioni non lineari

Esercizio: Gas Isoentropico

Il file es_isentropic.m contiene i dati del problema

Definite una funzione:

function z = f(p, T, p0, T0, gm, M, z0z, R, g)

• Che corrisponda al sistema di equazioni da risolvere…
• …Ma esponga tutti i parametri

Definite quindi una funzione anonima che esponga solo \(\gamma\) e \(M\)

• Usatela per determinare \(\gamma\) e \(M\)
• NOTA: Usando due funzioni (normale + anonima)
• …È molto veloce definire quali siano le variabili ed i parametri
• Le variabili sono quelle “esposte” nella funzione anonima!

Esercizio: Dodge-Metzner

Consideriamo un fluido di potenza (dilatante o pseudoplastico)

• Se il fluido è in moto turbolento, il fattore di attrito \(f\) in una condotta
• …è definito dalla seguente relazione (Dodge-Metzner):

\[\frac{1}{\sqrt{f}} = \frac{4}{n^{0.75}} \log\left(Re_{pl} f^{1 - n/2}\right) - \frac{0.4}{n^{1.2}}\]

• Dove \(n\) è un parametro che caratterizza il fluido
• \(Re_{pl}\) è un numero di Reynolds modificato

Vogliamo utilizzare la relazione per calcolare il valore di \(f\)

Si supponga che i valori di \(Re_{pl}\) e \(n\) siano noti

Esercizio: Dodge-Metzner

Il file es_dodge_metzner.m contiene i dati del problema

• Definite nel file una funzione ausiliaria:

function z = dodge_metzner(f, n, Re_pl)

• Dovremo rendere la funzione utilizzabile in fzero o fsolve…
• …usando una funzione anonima per esporre solo alcuni parametri
• Si disegni l’andamento della funzione da azzerare
• Si determini il valore di \(f\) con fzero o fsolve

In un secondo momento:

• Si assuma che \(f\) valga \(0.0020\)…
• …E si determini il valore corrispondente di \(n\)

Esercizio: Buckingham-Reiner

Consideriamo un fluido di Bingham

• Se il fluido è in moto laminare, il fattore di attrito \(f\) in una condotta
• …è definito dalla seguente relazione (Buckingham-Reiner):

\[f = \frac{64}{Re} \left(1 + \frac{1}{6}\frac{He}{Re} - \frac{64}{3} \frac{He^4}{f^3 Re^7} \right)\]

• Dove \(He\) è il numero di Hedstrom
• E \(Re\) è il numero di Reynolds

Vogliamo utilizzare la relazione per calcolare il valore di \(f\)

Si supponga che i valori di \(Re\) e \(He\) siano noti

Esercizio: Buckingham-Reiner

Il file es_buckingham_reiner.m contiene i dati del problema

• Definite nel file una funzione ausiliaria:

function z = buckingham_reiner(f, Re, He)

• Dovremo rendere la funzione utilizzabile in fzero o fsolve…
• …usando una funzione anonima per esporre solo alcuni parametri
• Si disegni l’andamento della funzione da azzerare
• Si determini il valore di \(f\) con fzero o fsolve

Attenzione: Per \(f = 0\) l’equazione perde senso fisico!

• Scegliete il range per il disegno di conseguenza
• Conviene usare più dei 100 punti che linspace usa di default