Laboratorio di Informatica T (Ch10)
Interpolazione Polinomiale Esatta
Interpolazione Polinomiale Esatta
Per il composto acido formico:
- Vogliamo determinare come varia la pressione di saturazione \(P^*\)…
- …In funzione della temperatura \(T\), sopra il punto di fusione
Abbiamo a disposizione i seguenti dati sperimentali:

- Vogliamo determinare la pressione per ogni temperatura
Un possibile approccio:
- Possiamo provare a tracciare una curva…
- …Che soddisfi tutte le osservazioni sperimentali
Interpolazione Polinomiale Esatta
Innanzitutto preparo i dati:
% Temperatura (°C) e Pressione (Torr)
T = [-20,-5,2.1,10.3,24,32.4,43.8,61.4,80.3,100.6];
P = [1, 5, 10, 20, 40, 60, 100, 200, 400, 760];
Tf = 8.2; % Temperatura di fusione (°C)
% Trasformo le temperature in °K
T = T + 273.15;
Tf = Tf + 273.15;
% Considero i punti sopra la temperatura di fusione
P = P(T > Tf) % Uso T per selezione una parte di P
T = T(T > Tf) % Quindi rimpiazzo T- Nota: per restringere il campo ai valori sopra la temperature di fusione…
- …Abbiamo usato una indicizzazione con vettore di valori logici
Interpolazione Polinomiale Esatta
Che tipo di curva andremo a costruire?
- Potremmo usare un polinomio…
- …Con un parametro per ogni osservazione sperimentale
Ragionando così, dovremmo usare un polinomio di 7° grado
\[\alpha_7 t_0^7 + \alpha_6 t_0^6 + \alpha_5 t_0^5 + \alpha_4 t_0^4 + \alpha_3 t_0^3 + \alpha_2 t_0^2 + \alpha_1 t_0 + \alpha_0 = p_0 \\ \alpha_7 t_1^7 + \alpha_6 t_1^6 + \alpha_5 t_1^5 + \alpha_4 t_1^4 + \alpha_3 t_1^3 + \alpha_2 t_1^2 + \alpha_1 t_1 + \alpha_0 = p_1 \\ \alpha_7 t_2^7 + \alpha_6 t_2^6 + \alpha_5 t_2^5 + \alpha_4 t_2^4 + \alpha_3 t_2^3 + \alpha_2 t_2^2 + \alpha_1 t_2 + \alpha_0 = p_2 \\ \ldots\]
- Un parametro \(\alpha_j\) per ogni monomio
- Una equazione per ogni coppia \(t_i, p_i\) di misurazioni
Interpolazione Polinomiale Esatta
A questo punto possiamo impostare un sistema lineare:
- Per costruire la matrice dei coefficienti…
- …Sfruttiamo il fatto che tutte le equazioni hanno la stessa struttura
Possiamo costruirla per concatenazione di colonne!
A questo punto possiamo risolvere il sistema:
Interpolazione Polinomiale Esatta
Questo tipo di problema è molto comune
Si parla di interpolazione polinomiale esatta
- Trovare una curva polinomiale…
- …Che intercetti una serie di punti noti…
- …E non debba soddisfare alcuna condizione addizionale
Matlab mette a disposizione una funzione per risolverli:
Xè il vettore con le coordinate \(x\)Yè il vettore con le coordinate \(y\)Pcontiene i coefficienti del polinomio interpolante
Interpolazione Polinomiale Esatta
Proviamo ad usarla:
Interpolazione Polinomiale Esatta
Purtroppo, il risultato lascia desiderare…
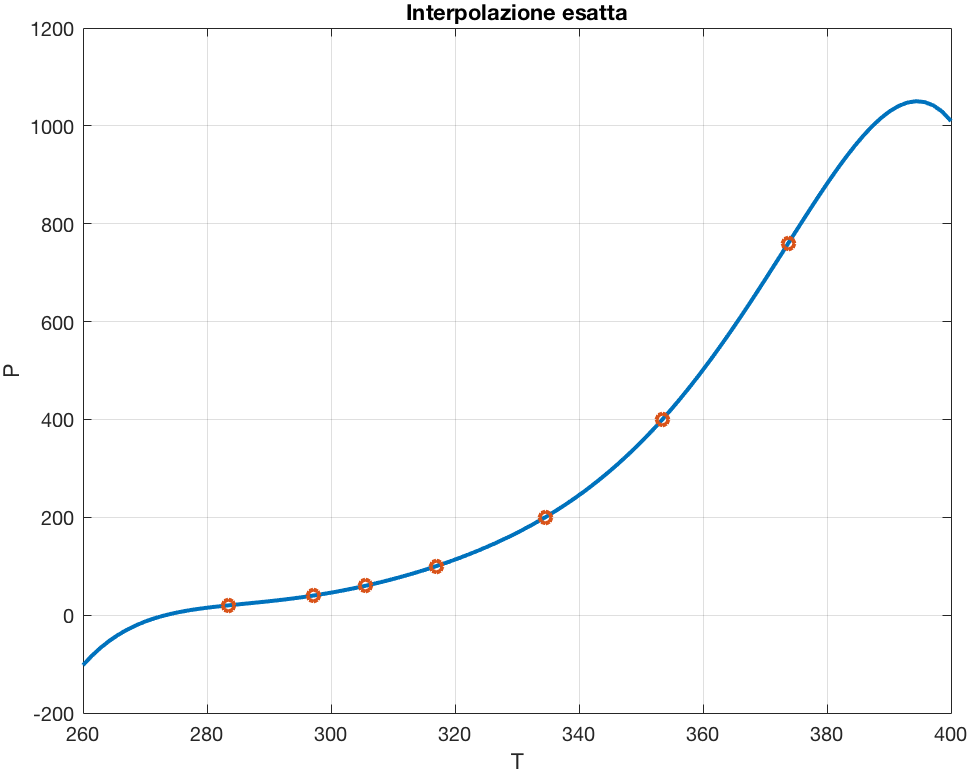
- All’“esterno” dei punti noti, l’andamento non ha senso fisico
- Il polinomio è di grado alto e può variare in modo troppo brusco
Interpolazione Lineare a Tratti
Interpolazione Lineare a Tratti
Come possiamo ovviare il problema?
Un primo approccio semplicissimo:
- Tra ogni coppia di misurazioni…
- …Assumiamo che la funzione sia lineare
Così otteniamo una approssimazione lineare a tratti
In Matlab la possiamo calcolare con:
X,Ysono le coordinate \(x\) ed \(y\) dei punti notixcontiene i valori di \(x\) per cui si desidera la valutazioneyè il valore dell’approssimazione nei punti desiderati
Interpolazione Lineare a Tratti
Nel nostro caso, potremmo avere:
Interpolazione Lineare a Tratti
Va molto meglio!
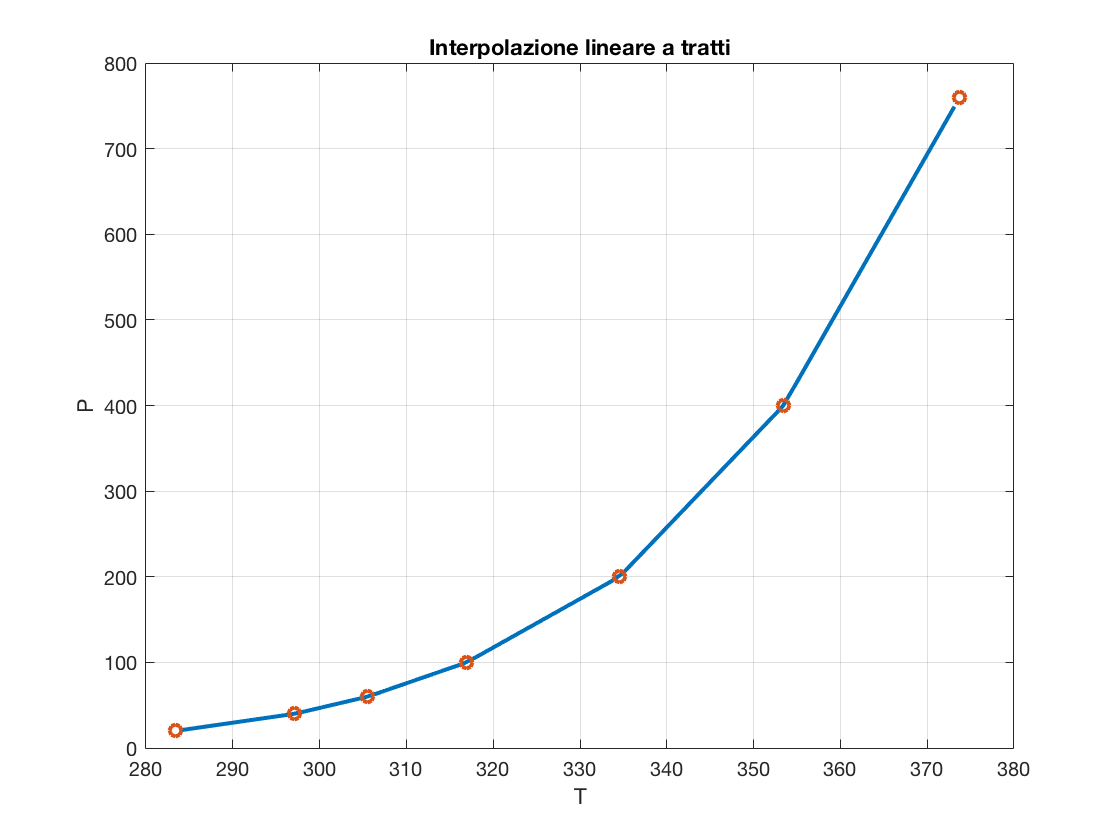
- Ma cosa succede all’esterno del range?
- E se abbiamo poche misurazioni? O se sono inaffidabili?
Metodo Lineare dei Minimi Quadrati
Metodo Lineare dei Minimi Quadrati
Idealmente, dovremmo limitare il grado dell’approssimazione
Per esempio, potremmo impostare:
\[\alpha_2 t_0^2 + \alpha_1 t_0 + \alpha_0 = p_0 \\ \alpha_2 t_1^2 + \alpha_1 t_1 + \alpha_0 = p_0 \\ \alpha_2 t_2^2 + \alpha_1 t_2 + \alpha_0 = p_0 \\ \alpha_2 t_3^2 + \alpha_1 t_3 + \alpha_0 = p_0 \\ \ldots\]
Alle equazioni corrisponde un sistema:
\[A x = b\]
- Purtroppo il sistema che si ottiene è tipicamente sovradeterminato
- Troppe equazioni, pochi gradi di libertà \(\Rightarrow\) nessuna soluzione
Metodo Lineare dei Minimi Quadrati
Metodo dei minimi quadrati
Potremmo però risolvere il sistema in senso approssimato:
- Misuriamo l’errore in base ai residui del sistema lineare
\[E = Ax - b\]
- Minimizziamo il quadrato della norma dell’errore:
\[\min_x \|E\|^2 = \min_x \|Ax-b\|^2\]
Perché il quadrato dell’errore?
- Considera come errore sia i residui positivi che quelli negativi
- Penalizza i grandi errori in modo maggiore
- Ma soprattutto, si deriva facilmente!
Metodo Lineare dei Minimi Quadrati
Il problema di minimizzazione:
\[\min_x \|Ax-b\|^2\]
Si riduce ad un secondo sistema lineare:
\[A^TA x = A^T b\]
Da cui si ottengono le cosiddette equazioni normali:
\[x = (A^TA)^{-1} A^T b\]
- Il risultato è il vettore \(x\) di coefficienti…
- …Che minimizza la somma dei quadrati dei residui
Intuitivamente: i coefficienti di una buona approssimazione
Metodo Lineare dei Minimi Quadrati
Quindi, possiamo impostare il problema come al solito
- Otteniamo una matrice
Acon più righe che colonne - Otteniamo una colonna
bdei termini noti
A questo punto, in teoria ci basta risolvere le equazioni normali:
In pratica, è ancora più semplice. Basta calcolare:
- Matlab si accorge che
Anon è quadrata… - …E risolve le equazioni normali (senza dirci niente)
Metodo Lineare dei Minimi Quadrati
Quindi, possiamo impostare il problema come al solito
- Otteniamo una matrice
Acon più righe che colonne - Otteniamo una colonna
bdei termini noti
A questo punto, in teoria ci basta risolvere le equazioni normali:
In pratica, è ancora più semplice. Basta calcolare:
- Attenzione: La sintassi utilizzata è la stessa della divisione sinistra
- Può trarre in inganno (e.g. e se il sistema è davvero sovradeterminato?)
Metodo Lineare dei Minimi Quadrati
In realtà, il metodo funziona se il sistema di partenza è lineare
Questo è vero se la funzione approssimante è nella forma:
\[f(x) = \sum_{j=0}^{n-1} \alpha_j g_j(x)\]
- I.e. una somma pesata di “funzioni base” \(g_j(x)\)
In generale, la nostra matrice dei coefficienti avrà questa struttura:
\[\left(\begin{array}{cccc} g_{n-1}(x_0) & g_{n-2}(x_0) & \ldots & g_{0}(x_0) \\ g_{n-1}(x_1) & g_{n-2}(x_1) & \ldots & g_{0}(x_1) \\ \vdots & \vdots & \ddots & \vdots \\ g_{n-1}(x_{m-1}) & g_{n-2}(x_{m-1}) & \ldots & g_{0}(x_{m-1}) \\ \end{array}\right)\]
- Una colonna per funzione base, una riga per data point
Metodo Lineare dei Minimi Quadrati
Torniamo a noi
Nel nostro esempio, sappiamo che vale l’equazione di Antoine:
\[P^* = e^{\left(a - \frac{b}{T}\right)}\]
- Dove \(a\) e \(b\) sono parametri da determinare empiricamente
- \(a\) è un coefficiente lineare, ma \(b\) no
- Quindi l’equazione non è nella forma corretta!
Metodo Lineare dei Minimi Quadrati
Torniamo a noi
Nel nostro esempio, sappiamo che vale l’equazione di Antoine:
\[P^* = e^{\left(a - \frac{b}{T}\right)}\]
- Dove \(a\) e \(b\) sono parametri da determinare empiricamente
- \(a\) è un coefficiente lineare, ma \(b\) no
- Quindi l’equazione non è nella forma corretta!
Fortunatamente, è facile adattarla:
\[\begin{align} & \ln P^* = a - \frac{b}{T} & \longrightarrow & & \ln P^* = a + b \left(-\frac{1}{T}\right) \end{align}\]
- In questo modo sia \(a\) che \(b\) sono coefficienti lineari
- Quindi possiamo applicare il metodo dei minimi quadrati!
Metodo Lineare dei Minimi Quadrati
Impostiamo un sistema come per l’interpolazione esatta
Quindi avremo:
\[a + b \left(-\frac{1}{T_0}\right) = \ln P^*_0 \\ a + b \left(-\frac{1}{T_1}\right) = \ln P^*_1 \\ \ldots\]
In forma matriciale:
\[\underbrace{\left(\begin{array}{cc} 1 & -\frac{1}{T_0} \\ 1 & -\frac{1}{T_1} \\ \ldots & \ldots \end{array}\right)}_{A} \left(\begin{array}{c} a \\ b \end{array}\right) = \underbrace{\left(\begin{array}{c} \ln P^*_0 \\ \ln P^*_1 \\ \ldots \end{array}\right)}_{b}\]
Metodo Lineare dei Minimi Quadrati
Nel codice:
Costruiamo la matrice \(A\) e la colonna \(b\) dei termini noti:
T = T' % Vettore delle temperature come colonna
A = [T.^0, -1./T]
b = log(P)' % Logaritmo delle temp. come colonnaRisolviamo le equazioni normali:
x(1)corrisponde ada,x(2)ab- Possiamo definire la funzione e disegnarla, e.g.
Metodo Lineare dei Minimi Quadrati
Nel nostro caso otteniamo:
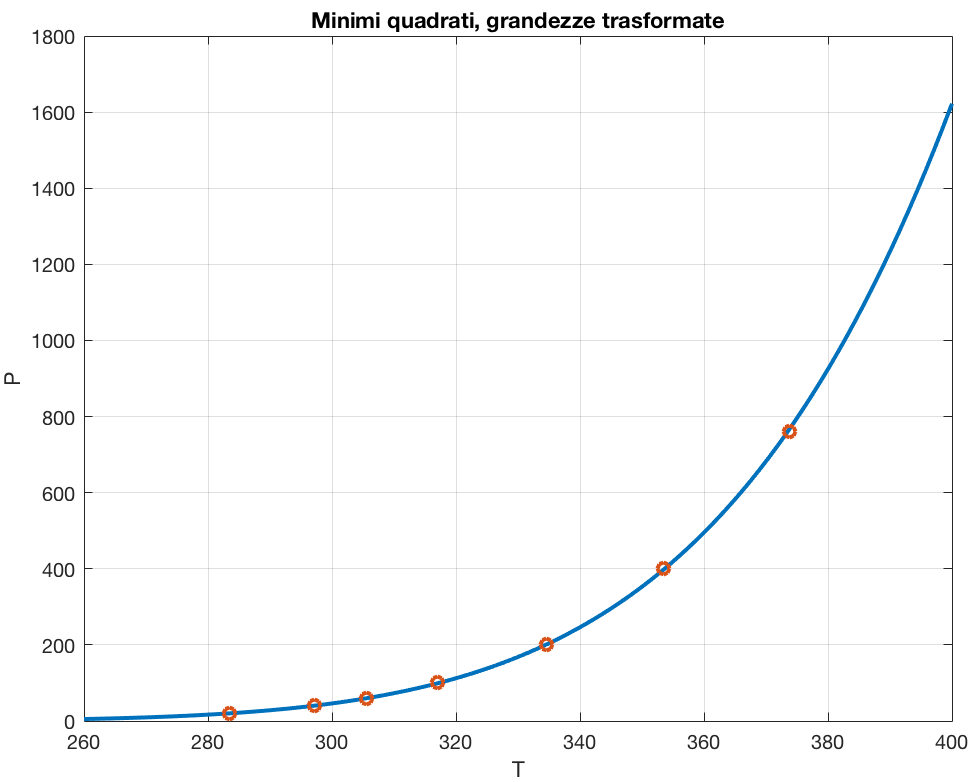
Es: Comportamento Reologico di un Fluido
Esercizio: Comp. Reologico di un Fluido
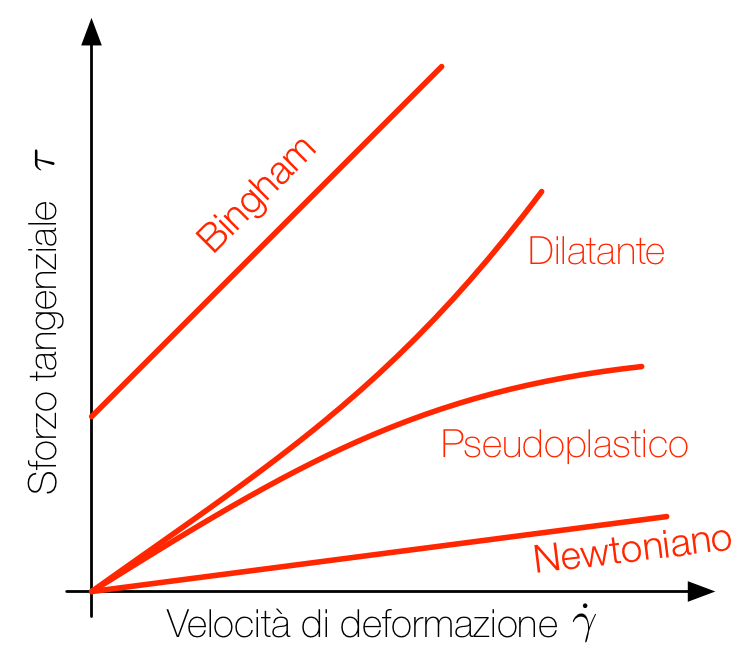
Si possono dividere i fluidi in diverse categorie…
- …In base alla relazione tra la velocità di deformazione \(\dot{\gamma}\)…
- …E lo sforzo tangenziale \(\tau\)
Esercizio: Comp. Reologico di un Fluido
In particolare, distinguiamo:
Fluidi Newtoniani, per cui:
\[\tau = a \dot{\gamma}\]
Fluidi di Bingham, per cui:
\[\tau = a \dot{\gamma} + b\]
Fluidi pseudoplastici e dilatanti, per cui:
\[\tau = b \dot{\gamma}^a\]
- Se \(a > 1\) il fluido è dilatante
- Se \(a < 1\) il fluido è pseudoplastico
Esercizio: Comp. Reologico di un Fluido
Per due fluidi, sono stati misurati i valori di \(\dot{\gamma}\) e \(\tau\)
- I dati sono disponibili nei file
fluid1.xlsxefluid2.xlsx - In Matlab si possono importare matrici da file Excel!
- Il file di script
es_fluidbehavior.mcontiene già il codice di lettura
Vogliamo determinare il tipo dei due fluidi. Per farlo:
Otterremo delle funzioni approssimanti \(f\) (via minimi quadrati)
- Verificheremo il valore del Mean Squared Error:
\[MSE = \frac{1}{n} \sum_{i = 1}^n (\tau_i - f(\dot{\gamma}_i))^2\]
È semplicemente la media dei residui al quadrato
- L’approssimazione con il minor MSE sarà tendenzialmente corretta
Esercizio: Comp. Reologico di un Fluido
Prima parte: verifica se il fluido sia di Bingham
Nel file es_fluidbehavior.m nello start-kit, definite la funzione:
function [MSE, f] = check_Bingham(DGAMMA, TAU)Che prenda come parametri:
- Un vettore riga
DGAMMAcon i valori noti di \(\dot{\gamma}\) - Un vettore riga
TAUcon i valori noti di \(\tau\)
La funzione assume che il fluido sia di Bingham e restituisce:
- In
MSEil Mean Squared Error - Una funzione
fche calcoli \(\tau = f(\dot{\gamma}) = a \dot{\gamma} + b\)
Esercizio: Comp. Reologico di un Fluido
Prima parte: verifica se il fluido sia di Bingham
Nel file es_fluidbehavior.m nello start-kit, definite la funzione:
function [MSE, f] = check_Bingham(DGAMMA, TAU)- Si esegua la funzione per i dati dei due fluidi
- Si utilizzi il parametro di uscita
fper disegnare:- La funzione approssimante, tra
min(DGAMMA)emax(DGAMMA) - I punti noti originali
- La funzione approssimante, tra
È possibile farlo utilizzando la funzione:
- Già definita nello start-kit
Esercizio: Comp. Reologico di un Fluido
Seconda parte: verifica se il fluido sia Newtoniano
Nel file es_fluidbehavior.m nello start-kit, definite la funzione:
function [MSE, f] = check_Newton(DGAMMA, TAU)Che prenda come parametri:
- Un vettore riga
DGAMMAcon i valori noti di \(\dot{\gamma}\) - Un vettore riga
TAUcon i valori noti di \(\tau\)
La funzione assume che il fluido sia Newtoniano e restituisce:
- In
MSEil Mean Squared Error - Una funzione
fche calcoli \(\tau = f(\dot{\gamma}) = a \dot{\gamma}\)
Esercizio: Comp. Reologico di un Fluido
Seconda parte: verifica se il fluido sia Newtoniano
Nel file es_fluidbehavior.m nello start-kit, definite la funzione:
function [MSE, f] = check_Newton(DGAMMA, TAU)- Si esegua la funzione per i dati dei due fluidi
- Si utilizzi il parametro di uscita
fper disegnare:- La funzione approssimante, tra
min(DGAMMA)emax(DGAMMA) - I punti noti originali
- La funzione approssimante, tra
È possibile farlo utilizzando la funzione:
- Già definita nello start-kit
Esercizio: Comp. Reologico di un Fluido
Terza parte: verifica se il fluido sia pseudoplastico o dilatante
Nel file es_fluidbehavior.m nello start-kit, definite la funzione:
function [MSE, f] = check_PowerLaw(DGAMMA, TAU)Che prenda come parametri:
- Un vettore riga
DGAMMAcon i valori noti di \(\dot{\gamma}\) - Un vettore riga
TAUcon i valori noti di \(\tau\)
La funzione assume che il fluido segua la legge \(\tau = b \dot{\gamma}^a\) e restituisce:
- In
MSEil Mean Squared Error - Una funzione
fche calcoli \(\tau = f(\dot{\gamma}) = b \dot{\gamma}^a\)
Esercizio: Comp. Reologico di un Fluido
Terza parte: verifica se il fluido sia pseudoplastico o dilatante
Nel file es_fluidbehavior.m nello start-kit, definite la funzione:
function [MSE, f] = check_PowerLaw(DGAMMA, TAU)- Si esegua la funzione per i dati dei due fluidi
- Si utilizzi il parametro di uscita
fper disegnare:- La funzione approssimante, tra
min(DGAMMA)emax(DGAMMA) - I punti noti originali
- La funzione approssimante, tra
È possibile farlo utilizzando la funzione:
- Già definita nello start-kit
Esercizio: Qualità del Vino
Esercizio: Qualità del Vino
I due file winequality-red.xlsx e winequality-white.xlsx…
…Contengono informazioni su una serie di vini portoghesi
- L’ultima colonna contiene una stima della qualità (range 1-10)
- Le altre colonne contengono il valore di alcune proprietà fisico/chimiche
Formalmente, ogni data point è una coppia \((x_i, y_i)\) in cui:
- \(y_i\) è la qualità del vino
- \(x_i\) un vettore con le proprietà del vino (i.e. \(x_{i,0}\), \(x_{i,1}\), etc.)
Vogliamo ottenere una approssimazione \(f(x)\) della qualità \(y\)
- A differenza del caso precedente, \(f(x\)) in questo caso è multivariata…
- …Semplicemente perché \(x\) è un vettore!
Esercizio: Qualità del Vino
Come gestire funzioni multivariate? Nel solito modo!
Il metodo lineare dei minimi quadrati si può applicare a funzioni nella forma:
\[f(x) = \sum_{j=0}^{n-1} \alpha_j g_j(x)\]
- Ogni \(\alpha_j\) è un peso (da determinare), ogni \(g_j(x)\) è una funzione base
Una funzione basa può utilizzare solo alcune componenti del vettore
Una scelta molto frequente:
\[f(x) = \sum_{j=0}^{n-1} \alpha_j x_j\]
- I.e. \(f(x)\) è una combinazione lineare delle componenti di \(x\)
Esercizio: Qualità del Vino
A partire dal file es_wine.m:
Approssimare la qualità del vino (rosso e bianco) con una funzione \(f(x)\) tale che:
\[f(x) = \sum_{j=0}^{n-1} \alpha_j x_j\]
- Andranno determinati la matrice dei coefficienti e la colonna dei termini noti
- Poi si potranno determinare i pesi \(\alpha_j\) con il metodo dei minimi quadrati
Una volta determinati i pesi:
- Disegnare (con
histogram) l’istogramma dell’errore di stima, i.e.:
\[err(x_i) = y_i - f(x_i)\]
- Disegnare (con
bar) un grafico a barre che mostri i valori dei pesi \(\alpha\) - …Le barre più grandi corrisponderanno alle proprietà più importanti!
Esercizio: Deformazione Meccanica
Esercizio: Deformazione Meccanica
Sono date delle misure di deformazione di un pezzo meccanico
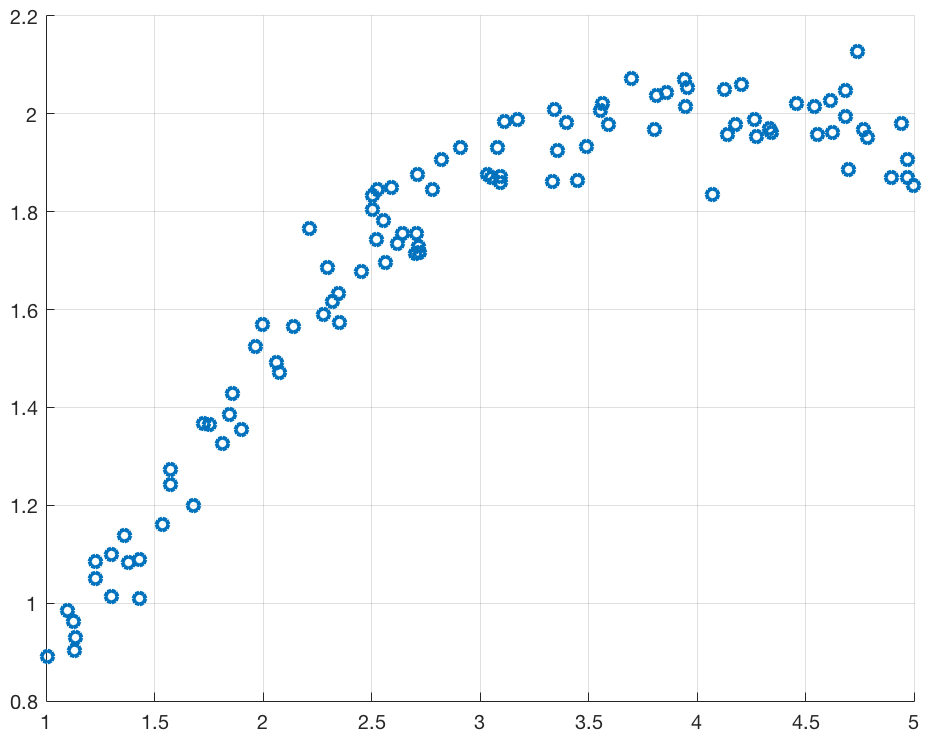
- Alle ascisse c’è la posizione originaria \(X\) di alcuni punti sul pezzo
- Alle ordinate c’è la posizione \(X2\) dopo la deformazione
Esercizio: Deformazione Meccanica
Le misure non sono molto precise (sono “rumorose”)
A partire dal file es_strain.m:
- Approssimare relazione \(X2 = F(X)\) con il metodo dei minimi quadrati
- Determinate (visivamente) il grado minimo necessario…
- …Per avere una approssimazione polinomiale adeguata
Una possibile definizione dello sforzo meccanico è data da:
\[S(X) = 1 - F'(X)\]
- Dove \(F'(X)\) è la derivata di \(F(X)\)
Si calcoli lo sforzo meccanico per \(X = 1.5\)
Esercizio: Velocità di un Fluido in Condotta
Esercizio: Velocità di un Fluido in Condotta
La velocità di un fluido in una condotta varia lungo la sezione
- Tendenzialmente, la velocità è maggiore al centro
- Il profilo di velocità è simile ad una parabola
Supponiamo di avere delle misurazioni di velocità
Le misurazioni sono nella forma \((x_i, y_i)\)
- \(x_i\) rappresenta la posizione sulla sezione della condotta
- \(y_i\) è il valore della velocità misurata
- Le posizioni degli estremi della condotta sono note
Vogliamo ricostruire l’intero profilo di velocità
Esercizio: Velocità di un Fluido in Condotta
Partite dal file es_waterspeed.m nello start-kit
Approssimate il profilo di velocità:
- Come funzione approssimante, utilizzate una parabola…
- …Quindi applicate il metodo dei minimi quadrati
Procedete poi a disegnare:
- Il valore del polinomio interpolante su tutta la condotta
- Utilizzando
scatterdisegnate anche le misurazioni
Provate quindi ad utilizzare una interpolazione polinomiale esatta
- Determinate il grado del polinomio necessario e disegnatelo
- Quale delle due curve vi sembra più realistica?
Esercizio: Prestazioni di una Pompa Centrifuga
Esercizio: Prestazione di una Pompa Centrifuga
Il diagramma di prestazione di una pompa centrifuga:

- Mostra la relazione tra la portata \(Q\) (alle ascisse)…
- …E la prevalenza \(H\) (una grandezza analoga alla pressione)
Esercizio: Prestazione di una Pompa Centrifuga
Spesso il diagramma viene definito a partire da valori noti, e.g.:

Nel file es_pump.m dello start-kit:
- Approssimare la curva utilizzando il metodo dei minimi quadrati
- Determinate (visivamente) il grado minimo necessario…
- …Per avere una approssimazione polinomiale adeguata
- Disegnate il polinomio approssimante ed i punti originari
- Determinate il valore di \(H\) per \(Q = 90\)
- Determinate lo stesso valore con una approssimazione lin. a tratti