Un Esempio (Moderatamente) Realistico

Consideriamo un ipotetico impianto di produzione di biodiesel:

Sommariamente, l'impianto funziona:

• Immettendo nutrienti ("cibo", C)...
• ...questi sono consumati da batteri (B)...
• ...che producono biodiesel (D)

In dettaglio le cose sono un po' più complesse...

Un Esempio (Moderatamente) Realistico

Nel dettaglio nell'impianto avvengono i seguenti processi:

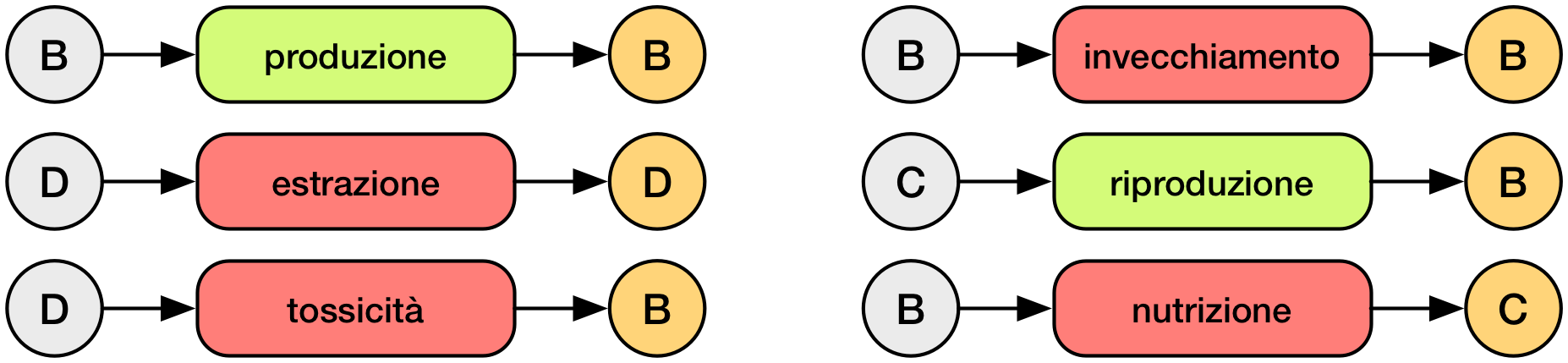
Ogni processo mette in relazione:

• La quantità dell'entità a sx (e.g. "D" per "tossicità")
• Con la quantità dell'entità a dx (e.g. "B" per "tossicità")

Verde: effetto positivo - Rosso: effetto negativo

Un Esempio (Moderatamente) Realistico

Nel dettaglio nell'impianto avvengono i seguenti processi:

In particolare, per ogni processo conosciamo:

• L'effetto sulla quantità dell'entità di dx...
• ...Misurato rispetto alla quantità dell'entità di sx

Un Esempio (Moderatamente) Realistico

Nel dettaglio nell'impianto avvengono i seguenti processi:

Il nostro problema:

• Se immettiamo costantemente nel sistema una unità di cibo...
• ...quante unità di biodiesel vengono prodotte a regime?

Come lo affrontiamo? Ci serve un modello matematico

Un Esempio (Moderatamente) Realistico

Questo è un esempio di un Sistema Dinamico:

• I "processi" descrivono l'evoluzione del sistema nel tempo
• Per ottenere un modello va deciso come trattare il tempo

Caso A: Consideriamo il tempo come una variabile continua

• Il modello consisterà di equazioni differenziali

Caso B: Consideriamo intervalli di tempo discreti

• Il modello consisterà di equazioni alle differenze

Questa volta vediamo solo il secondo caso

Un Esempio (Moderatamente) Realistico

Proviamo a tradurre i processi in equazioni

Usiamo $k$ per l'istante corrente e $k+1$ per il prossimo istante:

$$\begin{align} D^{(k+1)} & = (1 - \text{estr.})D^{(k)} + (\text{prod.})B^{(k)}\\ B^{(k+1)} & = (-\text{toss.}) D^{(k)} + (1-\text{inve.})B^{(k)} + (\text{ripr.}) F^{(k)}\\ C^{(k+1)} & = (-\text{nutr.})B^{(k)} + 1 C^{(k)} + \text{cibo introdotto} \end{align}$$

Un Esempio (Moderatamente) Realistico

Proviamo a tradurre i processi in equazioni

Introducendo i valori noti otteniamo:

$$\begin{align} D^{(k+1)} & = (1 - 1)D^{(k)} + 1 B^{(k)}\\ B^{(k+1)} & = -0.5 D^{(k)} + (1-0.2)B^{(k)} + 0.3 F^{(k)}\\ C^{(k+1)} & = -1 B^{(k)} + 1 C^{(k)} + 1 \end{align}$$

Un Esempio (Moderatamente) Realistico

Proviamo a tradurre i processi in equazioni

Alla fine otteniamo le seguenti equazioni alle differenze:

$$\begin{align} D^{(k+1)} & = B^{(k)}\\ B^{(k+1)} & = -0.5 D^{(k)} + 0.8 B^{(k)} + 0.3 F^{(k)}\\ C^{(k+1)} & = -1 B^{(k)} + 1 C^{(k)} + 1 \end{align}$$

Un Esempio (Moderatamente) Realistico

Proviamo a tradurre i processi in equazioni

Le equazioni sono lineari, quindi il nostro sistema dinamico è lineare

$$\begin{align} D^{(k+1)} & = B^{(k)}\\ B^{(k+1)} & = -0.5 D^{(k)} + 0.8 B^{(k)} + 0.3 F^{(k)}\\ C^{(k+1)} & = -1 B^{(k)} + 1 C^{(k)} + 1 \end{align}$$

Un Esempio (Moderatamente) Realistico

Proviamo a tradurre i processi in equazioni

Visto che il sistema è lineare, possiamo usare la forma matriciale:

$$\left(\begin{array}{c} D^{(k+1)}\\ B^{(k+1)}\\ C^{(k+1)}\\ \end{array}\right) = \left(\begin{array}{ccc} 0 & 1 & 0\\ -0.5 & 0.8 & 0.3\\ 0 & -1 & 1 \end{array}\right) \left(\begin{array}{c} D^{(k)}\\ B^{(k)}\\ C^{(k)}\\ \end{array}\right) + \left(\begin{array}{c} 0\\ 0\\ 1\\ \end{array}\right)$$

Elementi di Informatica e
Applicazioni Numeriche T

Stato Stazionario e Sistemi Lineari

Sistemi Dinamici Lienari

Generalizzando un po', il nostro sistema si presenta così:

$$x^{(k+1)} = Ax^{(k)} + b$$

• Dove la matrice $A$ è (sempre) quadrata
• Formalmente:

$$A: V \rightarrow V$$

• $A$ ci dice quale sarà il prossimo stato del sistema
• Per questo si chiama anche matrice di transizione (di stato)

Stato Stazionario di un Sistema Dinamico

• A noi interessa quanto biodiesel viene prodotto a regime...
• ...Ossia quando il comportamento del sistema di stabilizza

Questa condizione si chiama stato stazionario del sistema

Come possiamo individuare lo stato stazionario?

• Nello stato stazionario $x$ non cambia, ossia:

$$x^{(k+1)} = x^{(k)}$$

• Quindi possiamo riferci sia a $x^{k}$ che $x^{k+1}$ semplicemente con $x$:

$$x = Ax + b$$

Stato Stazionario di un Sistema Dinamico

• A noi interessa quanto biodiesel viene prodotto a regime...
• ...Ossia quando il comportamento del sistema di stabilizza

Questa condizione si chiama stato stazionario del sistema

Come possiamo individuare lo stato stazionario?

• Con qualche trasformazione otteniamo:

$$x - Ax = b$$

• E in forma matriciale:

$$(I - A)x = b$$

Stato Stazionario e Sistemi di Equazioni Lineari

Abbiamo ottenuto un normale sistema di equazioni lineari!

$$(I - A)x = b$$

La soluzione è data da:

$$x = (I - A)^{-1}b$$

• Si può risolvere per esempio usando la riduzione di Gauss
• Oppure invertendo la matrice (brutta idea: vedremo perché)

Se $A$ è non singolare, lo stato stazionario è unico

• Perché ci sono tanti vincoli quante variabili
• Noi assumeremo sempre che $A$ sia non singolare

Sistemi di Equazioni Lineari in Octave

Risolvere sistemi di equazioni lineari in Octave è facile

Si può usare l'operatore di divisione a sinistra "\"

X \ Y

• $X$ è una matrice che dovrebbe essere invertibile (non singolare)
• $Y$ è un vettore o una matrice
• e X \ Y sta per $X^{-1}Y$

Il risultato viene calcolato senza invertire la matrice X

Esiste anche un operatore di "divisione a destra":

• X / Y sta per $X Y^{-1}$

Sistemi di Equazioni Lineari in Octave

Nel nostro caso abbiamo:

$$x^* = (I - A)^{-1}b$$

Dove $x^*$ è lo stato stazionario. Si può risolvere con:

n = rows(A);
x = (eye(n) - A) \ b

• eye(n) restituisce la matrice identità $n\times n$

Con la nostra matrice $A$ e vettore $b$ il risultato è:

$$x^* = (D^*, B^*, C^*) = (1, 1, 2.334)$$

• Quindi a regime viene prodotta una unità di biodiesel

Elementi di Informatica e
Applicazioni Numeriche T

Iterazione di Punto Fisso

Un Metodo di Soluzione Alternativo

Vediamo un metodo alternativo per trovare lo stato stazionario

Consideriamo il sistema dinamico lineare:

$$x^{(k+1)} = A x^{(k)} + b$$

Possiamo lasciare evolvere il sistema finché non ci arriva da solo

Iterazione di Punto Fisso

L'algoritmo si chiama Iterazione di Punto Fisso

È molto facile da codificare:

x = rand(n, 1); % n = num. variabili
x_old = -Inf
while x ~= x_old
    x_old = x;
    x = A * x + b;
end

Il confronto x ~= x_old è molto "pericoloso" perché:

• Lo stato stazionario può essere raggiunto asintoticamente
• Se succede x e x_old non saranno mai uguali!

Iterazione di Punto Fisso

L'algoritmo si chiama Iterazione di Punto Fisso

È molto facile da codificare:

x = rand(n, 1); % n = num. variabili
x_old = -Inf
while x ~= x_old
    x_old = x;
    x = A * x + b;
end

Il confronto x ~= x_old è molto "pericoloso" perché:

• x e x_old sono rappresentati con un numero finito di bit
• I calcoli sono inevitabilmente approssimati!

Iterazione di Punto Fisso

L'algoritmo si chiama Iterazione di Punto Fisso

È molto facile da codificare:

x = rand(n, 1); % n = num. variabili
x_old = -Inf
while abs(x - x_old) > 10e-6 % era: x ~= x_old
    x_old = x;
    x = A * x + b;
end

Soluzione: usare $|x^{(k+1)} - x^{(k)}| > \varepsilon$

• Per $\varepsilon$ si usa un valore di tolleranza arbitrario
• Nel codice è stato scelto $10^{-6}$

Iterazione di Punto Fisso: Osservazioni

A proposito dell'approssimazione:

• L'algoritmo otterrà in genere delle soluzioni approssimate
• Ma anche il sistema di equazioni lineari!

I numeri sono sempre rappresentati con un numero finito di bit

• Quindi una certa approssimazione è inevitabile!
• ...Perlomeno quando lavoriamo con numeri in virgola mobile

È una osservazione importante e generale

• Una conseguenza: fidatevi poco dei confronti di tipo x == y
• Meglio usare abs(x-y) < tolleranza

Iterazione di Punto Fisso: Osservazioni

Perchè si chiama "Iterazione di Punto Fisso"

Consideriamo la descrizione del nostro stato stazionario:

$$x = Ax + b$$

• $x$ viene mappato da $Ax + b$ in sé stesso
• Si dice che $x$ è un punto fisso di $Ax+b$

Possiamo vedere la cosa da due punti di vista:

• Lo stato stazionario del sistema dinamico $x^{(k+1)} = Ax^{(k)} + b$
• Oppure il punto fisso di $Ax + b$

Iterazione di Punto Fisso: Osservazioni

Tale equivalenza è molto importante

Se abbiamo un sistema di equazioni lineari nella forma:

$$x = Ax + b$$

• Possiamo vederlo come un sistema dinamico:

$$x^{(k+1)} = Ax^{(k)} + b$$

• Ed applicare l'IPF per risolverlo

L'avevamo già detto, ma vale la pena di ripeterlo

Elementi di Informatica e
Applicazioni Numeriche T

Convergenza e Divergenza

Prestazioni dell'IPF

Come si comporta l'Iterazione di Punto Fisso nel nostro caso?

Ricapitoliamo un po' la situazione:

$$\begin{align} A &= \left(\begin{array}{ccc} 0 & 1 & 0\\ -0.5 & 0.8 & 0.3\\ 0 & -1 & 1 \end{array}\right) & b &= \left(\begin{array}{c} 0\\ 0\\ 1\\ \end{array}\right) \end{align}$$

Il punto fisso/stato stazionario è dato da:

$$x^* = (I - A)^{-1}b = (1, 1, 2.334)^T$$

Quanto velocemente ci arriva IPF?

Prestazioni dell'IPF

100 iterazioni di IPF (blu = partenza, rosso = punto fisso)

Prestazioni dell'IPF

• Non siamo andati malaccio!
• In qualche decina di iterazioni siamo arrivati al punto fisso...
• Ossia, l'algoritmo è arrivato a convergenza

Non va sempre così bene, però...

A volte ci vogliono molte iterazioni per convergere

• Si dice anche che la convergenza è "lenta"
• Ovviamente, se il vettore è vicino al punto iniziale...
• ...ci vorranno meno iterazioni per convergere

Può essere anche che IPF non converga affatto...

Convergenza e Divergenza

Consideriamo una piccola variazione del nostro sistema:

Portiamo la mortalità per invecchiamento al 5% (invece che 20%):

$$\begin{align} A &= \left(\begin{array}{ccc} 0 & 1 & 0\\ -0.5 & \bf 0.95 & 0.3\\ 0 & -1 & 1 \end{array}\right) & b &= \left(\begin{array}{c} 0\\ 0\\ 1\\ \end{array}\right) \end{align}$$

Il punto fisso/stato stazionario è dato da:

$$x^* = (I - A)^{-1}b = (1, 1, 1.834)^T$$

Vediamo come si comporta IPF in questo caso...

Convergenza e Divergenza

L'IPF si allontana dal punto fisso, cioè diverge

Convergenza e Divergenza

Vediamo un'altra variazione:

Portiamo la mortalità per invecchiamento al 10% (invece che 20%):

$$\begin{align} A &= \left(\begin{array}{ccc} 0 & 1 & 0\\ -0.5 & \bf 0.9 & 0.3\\ 0 & -1 & 1 \end{array}\right) & b &= \left(\begin{array}{c} 0\\ 0\\ 1\\ \end{array}\right) \end{align}$$

Il punto fisso/stato stazionario è dato da:

$$x^* = (I - A)^{-1}b = (1, 1, 2)^T$$

Vediamo come si comporta l'IPF in questo caso...

Convergenza e Divergenza

L'IPF assume un comportamento periodico

Convergenza, Divergenza ed Equilibri

Ci sono tre comportamenti possibili:

Sono interpretabili in termini di:

• Punto fisso di una trasformazione lineare $Ax + b$
• Stato di un sistema dinamico

Caso 1: L'IPF converge

• In questo caso troviamo il punto fisso
• Lo stato stazionario rappresenta un equilibrio stabile

Di solito è il comportamento più desiderabile

Convergenza, Divergenza ed Equilibri

Caso 2: L'IPF diverge

• In questo caso non troviamo il punto fisso di $Ax + b$
• Lo stato stazionario rappresenta un equilibrio instabile
• Una perturbazione dell'equilibrio causa grandi variazioni

Di solito è il caso meno desiderabile

Caso 3: L'IPF assume un comportamento periodico

• In questo caso non troviamo il punto fisso di $Ax + b$
• Lo stato stazionario rappresenta un equilibrio instabile
• Una perturbazione dell'equilibrio causa oscillazioni finite

Gestire Casi di Non Convergenza

Possiamo modificare il codice per gestire casi non convergenti

Il nostro codice attuale:

x = rand(n, 1); % n = num. variabili
x_old = -Inf
while abs(x - x_old) > 10e-6
    x_old = x;
    x = A * x + b;
end

Gestire Casi di Non Convergenza

Possiamo modificare il codice per gestire casi non convergenti

Spostiamo il controllo di convergenza:

x = rand(n, 1); % n = num. variabili
x_old = -Inf
while % ???
    x_old = x;
    x = A * x + b;
    if abs(x - x_old) < 10e-6
        break
    end
end

Gestire Casi di Non Convergenza

Possiamo modificare il codice per gestire casi non convergenti

Usiamo un ciclo for per limitare le iterazioni

x = rand(n, 1); % n = num. variabili
x_old = -Inf
for k = 1:10000
    x_old = x;
    x = A * x + b;
    if abs(x - x_old) < 10e-6
        break
    end
end

Gestire Casi di Non Convergenza

Possiamo modificare il codice per gestire casi non convergenti

È buona norma usare delle variabili per aumentare la leggibilità

x = rand(n, 1); % n = num. variabili
x_old = -Inf
n = 10000; % limite di iterazione
tol = 10e-6; % tolleranza
for k = 1:n
    x_old = x;
    x = A * x + b;
    if abs(x - x_old) <= tol
        break
    end
end

Convergenza ed Errore

È possibile caratterizzare le condizioni di convergenza?

• Sì, ma bisogna arrivarci per gradi...
• ...come primo passo, è utile introdurre il concetto di errore

L'errore commesso dell'IPF ad una data iterazione è:

$$e = (x - x^*)$$

• Dove $x^*$ è il punto fisso

A cosa ci serve questa definizione?

• Proviamo a descrivere il nostro sistema in termini di errore...

Convergenza ed Errore

Il sistema è definito da:

$$x = Ax + b$$

• Con qualche manipolazione otteniamo:

$$x-x^* = A(x - x^* + x^*) + b - x^*$$

• Tenendo conto che $e = x - x^*$ otteniamo:

$$e = Ae + Ax^* + b - x^*$$

• Ma $x^*$ è un punto fisso, quindi $A x^* + b = x^*$, quindi:

$$e = A e$$

Dimostrazione di Convergenza

Come cambia l'errore nel tempo?

• Basta vedere il punto fisso come stato stazionario:

$$e^{(k+1)} = A e^{(k)}$$

• Perché vi sia convergenza l'errore deve decrescere:

$$\lim_{k \rightarrow \infty} \frac{\left| e^{(k+1)} \right|}{\left| e^{(k)} \right|} < 1$$

• Noi sappiamo che $e^{(k+1)} = A e^{(k)}$ e quindi:

$$\lim_{k \rightarrow \infty} \frac{\left| A e^{(k)} \right|}{\left| e^{(k)} \right|} < 1$$

Dimostrazione di Convergenza

Per semplicità:

• Consideriamo solo il caso in cui $A$ sia diagonalizzabile
• Quindi, esiste una matrice di cambiamento di base $P$ tale che:

$$A = P^{-1} \Lambda P$$

• Dove $\Lambda$ è una matrice diagonale...
• ...e gli elementi sulla diagonale sono gli autovalori $\lambda_i$

Quindi possiamo scrivere:

$$\lim_{k \rightarrow \infty} \frac{\left| P^{-1}\Lambda P e^{(k)} \right|}{\left| e^{(k)} \right|} < 1$$

Dimostrazione di Convergenza

Tutto dipende dal valore di $\left|P^{-1}\Lambda P e^{(k)}\right|$ e $\left|e^{(k)}\right|$

• Poiché $P$ è una matrice di cambiamento di base...
• I vettori $Pv$ e $P^{-1}v$ hanno lo stesso valore assoluto di $v$

Quindi il termine:

$$\left|P^{-1}\Lambda P e^{(k)}\right|$$

• Ha un valore assoluto più piccolo di $\left|e^{k}\right|$ se e solo se...
• ...tutti gli elementi di $\Lambda$ hanno un valore assoluto $< 1$

Quindi se per tutti gli autovalori $\lambda_i$ di $A$ vale $|\lambda_i| < 1$

Convergenza ed Autovalori

In Octave, basta controllare che siano $< 1$ tutti gli elementi di:

abs(eig(A))

• eig(A) restituisce gli autovalori di $A$

Cosa succede se c'è un autovalore con $|\lambda_i| \geq 1$?

Se $|\lambda_i| > 1$, allora:

• IPF diverge/lo stato stazionario è instabile

Se $|\lambda_i| = 1$, allora:

• IPF/il sistema dinamico hanno comportamento periodico

Qualche Dritta

Se siete interessati ad un caso specifico, e.g.:

• Trovare lo stato stazionario di un particolare sistema
• Risolvere uno specifico sistema di equazioni

Potete anche non stare a calcolare gli autovalori

• Eseguite IPF e vedete se funziona
• Basta tenere traccia dei valori di $x^{(k)}$...
• ...e si deduce da quelli se ci sia convergenza o no

Elementi di Informatica e
Applicazioni Numeriche T

IPF ed Equazioni Non Lineari

Partiamo da un Problema

Supponiamo di dover risolvere una equazione non lineare

Per esempio (un ipotetico bilancio di energia):

$$\log (x+1) = x^2-1$$

Partiamo da un Problema

Supponiamo di dover risolvere una equazione non lineare

Si tratta di trovare un punto in cui le due curve si intersecano

Partiamo da un Problema

Supponiamo di dover risolvere una equazione non lineare

Per esempio (un ipotetico bilancio di energia):

$$\log (x+1) = x^2-1$$

• Non esiste una soluzione generale in forma chiusa
• Che possiamo fare?

Partiamo da un Problema

Supponiamo di dover risolvere una equazione non lineare

Per esempio (un ipotetico bilancio di energia):

$$\log (x+1) = x^2-1$$

• Non esiste una soluzione generale in forma chiusa
• Che possiamo fare?

Proviamo a manipolarla un po':

$$\begin{align} x+1 &= e^{x^2-1}\\ x &= e^{x^2-1} - 1 \end{align}$$

E qui ci fermiamo. Perché?

IPF ed Equazioni Non Lineari

Possiamo vedere l'equazione come un sistema dinamico...

$$x^{(k+1)} = e^{(x^{(k)})^2-1} - 1$$

...e tentare di risolverlo con l'Iterazione di Punto Fisso

• Se il metodo converge, otteniamo una soluzione approssimata
• Se non converge, non abbiamo nulla

Ricordiamo però che:

• Per le equazioni non lineari generiche...
• ...una soluzione in forma chiusa non esiste

Una soluzione in alcuni casi è sempre meglio che niente!

IPF ed Equazioni Non Lineari

Possiamo vedere l'equazione come un sistema dinamico...

$$x^{(k+1)} = e^{(x^{(k)})^2-1} - 1$$

...e tentare di risolverlo con l'Iterazione di Punto Fisso

L'approccio è applicabile ad equazioni generiche di tipo:

$$x = f(x)$$

...Purché il dominio ed il codominio coincidano: $f : V \rightarrow V$

• Caso 1: $x$ scalare ed $f(x)$ scalare
• Caso 2: $x$ vettore ed $f(x)$ vettore (stessa dimensione)

IPF ed Equazioni Non Lineari

Il codice è praticamente invariato:

x = rand(n, 1); % n = num. variabili
x_old = -Inf
n = 10000;
tol = 10e-6;
for k = 1:n
    x_old = x;
    x = f(x); % <-- Era: A * x + b
    if abs(x - x_old) <= tol
        break
    end
end

Un Esempio di Esecuzione

Visualizziamo l'esecuzione di IPF con funzioni ad un variabile:

Un Esempio di Esecuzione

Tracciamo $y = f(x)$, $y=x$ ed il punto di partenza $x^{(0)}$ (in rosso)

Un Esempio di Esecuzione

Primo passo: calcoliamo $f(x^{(0)})$

Un Esempio di Esecuzione

Primo passo: $f(x^{(0)})$ diventa il valore di $x^{(1)}$

Un Esempio di Esecuzione

Secondo passo: calcoliamo $f(x^{(1)})$

Un Esempio di Esecuzione

Secondo passo: $f(x^{(1)})$ diventa il valore di $x^{(2)}$

Un Esempio di Esecuzione

Terzo passo: calcoliamo $f(x^{(2)})$

Un Esempio di Esecuzione

Procediamo fino a convergenza (o fino al limite di iterazioni)

Convergenza (Caso Non Lineare)

Se $f(x)$ è non lineare, può esserci più di un punto fisso

In altre parole, più soluzioni per:

$$x = f(x)$$

Ogni punto fisso può rappresentare:

• Un equilibrio stabile
• Un equilibrio instabile

Nel secondo caso, il punto fisso è raggiunto solo se $x^{(0)} = x^*$

• Di fatto: la soluzione è praticamente irraggiungibile

Convergenza (Caso Non Lineare)

Se $f(x)$ è non lineare, può esserci più di un punto fisso

In altre parole, più soluzioni per:

$$x = f(x)$$

Inoltre, a seconda della scelta di $x^{(0)}$

• IPF può convergere ad un punto fisso diverso
• Oppure IPF può divergere

Condizione di convergenza per un punto $x^*$ (caso scalare):

• Il valore iniziale $x^{(0)}$ è vicino ad $x^*$
• La derivata $\left|f'(x)\right|$ è $< 1$ in un intorno di $x^*$

Convergenza (Caso Non Lineare)

Proviamo ad abbozzare una dimostrazione:

• Per avere convergenza, deve valere

$$\lim_{k \rightarrow \infty} \frac{|e^{(k+1)}|}{|e^{(k)}|} < 1$$

• Quindi:

$$\lim_{k \rightarrow \infty} \frac{|x^{(k+1)} - x^*|}{|x^{(k)} - x^*|} < 1$$

Convergenza (Caso Non Lineare)

Proviamo ad abbozzare una dimostrazione:

• Quando eseguiamo IPF, abbiamo $x^{(k+1)} = f(x^{(k)})$:

$$\lim_{k \rightarrow \infty} \frac{|f(x^{(k)}) - x^*|}{|x^{(k)} - x^*|} < 1$$

• Poiché $x^*$ è un punto fisso, abbiamo $x^* = f(x^*)$

$$\lim_{k \rightarrow \infty} \frac{|f(x^{(k)}) - f(x^*)|}{|x^{(k)} - x^*|} < 1$$

In sostanza, la pendenza di $f(x)$ nei punti visitati deve essere $< 1$

Convergenza (Caso Non Lineare)

Proviamo ad abbozzare una dimostrazione:

• In particolare, quando siamo molto vicini ad $x^*$:

$$\frac{|f(x^{(k)}) - f(x^*)|}{|x^{(k)} - x^*|} \longrightarrow |f'(x)|$$

• Così arriviamo al nostro risultato...

Il modulo di $f'(x)$ deve essere $< 1$ in un intorno di $x^*$

Punti Fissi Multipli: Esempio

Nel nostro caso:

Punti Fissi Multipli: Esempio

• Il punto fisso a sx è stabile ($|f'(x)| < 1$ in un intorno)

Punti Fissi Multipli: Esempio

• Il punto fisso a dx è instabile (non vale $|f'(x)| < 1$ in un intorno)

Punti Fissi Multipli: Esempio

• Se $x^{(0)}$ è troppo piccolo o troppo grande, si ha divergenza

Effetto di Manipolazioni Algebriche

Ci sono sempre molti modi per manipolare una equazione

Consideriamo il nostro esempio:

$$\log (x+1) = x^2-1$$

Aggiungendo $x$ da entrambi i lati, possiamo ottenere:

• $x = - \log (x+1) + (x^2-1) + x$
• $x = + \log (x+1) - (x^2-1) + x$

Invertendo $x^2 - 1$, possiamo ottenere invece:

• $x = \sqrt{\log (x+1) + 1}$
• Con l'assunzione che $\log (x+1) + 1 \geq 0$

Effetto di Manipolazioni Algebriche

Manipolazioni diverse possono portare a proprietà diverse

Possiamo sfruttare questo fatto a nostro vantaggio

• Consideriamo la forma $x = \sqrt{\log (x+1) + 1}$
• Potrebbe sembrare scomoda, perché richiede $\log (x+1) + 1 \geq 0$
• Però rende stabile il punto fisso di destra!

Effetto di Manipolazioni Algebriche

Stavolta abbiamo $|f(x)| < 1$ in un intorno del punto fisso dx

Effetto di Manipolazioni Algebriche

Manipolazioni diverse possono portare a proprietà diverse

Possiamo sfruttare questo fatto a nostro vantaggio

• Consideriamo la forma $x = \sqrt{\log (x+1) + 1}$
• Potrebbe sembrare scomoda, perché richiede $\log (x+1) + 1 \geq 0$
• Però rende stabile il punto fisso di destra!

Una Dritta per un Caso Frequente

Supponiamo di avere una equazione nella forma:

$$f(x) = g(x)$$

Due modi per trasformala in forma utile ad IPF sono:

• Invertire $f(x)$, ottenendo $x = f^{-1}(g(x))$
• Invertire $g(x)$, ottenendo $x = g^{-1}(f(x))$

Quale scegliere? Un possibile metodo:

• Disegnare (anche a mano) un grafico stile-IPF...
• ...Utilizzando direttamente $y = f(x)$ e $y = g(x)$...
• ...anziché $y = x$ (la bisettrice) ed un'altra funzione

Una Dritta per un Caso Frequente

Partiamo dalle due funzioni (blu = $f(x)$, rosso = $g(x)$)

Una Dritta per un Caso Frequente

Disegniamo un grafico stile-IPF, facendo sponda su $g(x)$

Una Dritta per un Caso Frequente

I movimenti verticali corrispondono a calcolare una funzione

Una Dritta per un Caso Frequente

I movimenti orizzontali corrispondono ad invertire una funzione

Una Dritta per un Caso Frequente

Così capiamo che invertendo $f(x)$ convergiamo al punto fisso di sx

Una Dritta per un Caso Frequente

Mentre invertendo $g(x)$ convergiamo al punto fisso di dx

Elementi di Informatica e
Applicazioni Numeriche T

Wrap-up

Wrap-up

Abbiamo visto un metodo di soluzione (IPF)

Può essere utilizzato per:

• Trovare lo stato stazionario di un sistema dinamico
• Trovare il punto fisso di una funzione

Partendo da una descrizione del sistema nella forma:

$$x = f(x)$$

• Ogni equazione può essere portata in questa forma...
• ...purché il dominio ed il codominio coincidano

Possiamo così risolvere numericamente equazioni anche non-lineari!

Wrap-up

L'Iterazione di Punto Fisso:

• Può convergere, divergere o assumere comportamento periodico
• Manipolando l'equazione si possono ottenere comportamenti diversi
• In generale, produce risultati approssimati

Conseguenze sulle condizioni di interruzione:

• Interrompiamo IPF dopo un certo numero di iterazioni...
• ...O se la differenza tra $x^{(k+1)}$ e $x^{(k)}$ è sotto un certa tolleranza

Attenzione al valore della tolleranza!

• Una convergenza lenta può far interrompere IPF troppo presto