Progettare Algoritmi

Ci sono due approcci fondamentali per progettare algoritmi

Servono ambedue ad aiutarci ad affrontare il problema

• Si chiamano "top-down" e "bottom-up"
• Sono logicamente opposti...
• ...ma in pratica si usano sempre in modo combinato

Nelle prossime slide:

• Li definiremo in modo concettuale
• Poi mostreremo un esempio

Approccio Top-Down

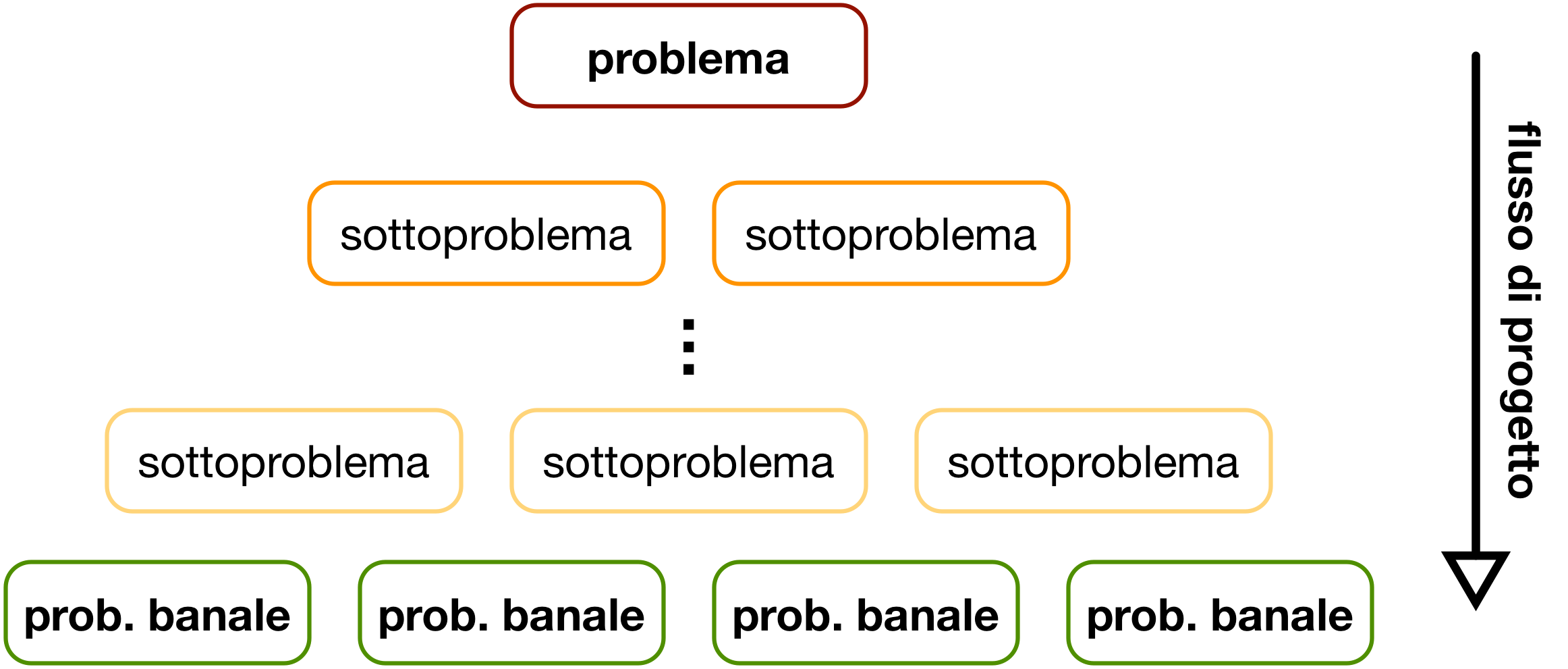
• Si parte dal problema iniziale
• Lo si decompone in sottoproblemi
• Finché questi non diventano banali da risolvere

Approccio Bottom-Up

• Si parte dalla funzioni disponibili
• Le si usano per risolvere problemi semplici
• Fino a risolvere il problema iniziale

Un Esempio: Confronto Di Parole

Problema: confrontare due stringhe della stessa lunghezza

Obiettivo: definire una funzione "strcmp":

strcmp('cane', 'casa')

Risultato:

• < 0 se la prima parola precede la seconda
• 0 se sono uguali
• > 0 se la seconda parola precede la prima

Un Esempio: Confronto Di Parole

Approccio (tendenzialmente) top-down:

Partiamo dal problema:

function z = strcmp(p1, p2)
  z = <confronto>;
end

Un Esempio: Confronto Di Parole

Approccio (tendenzialmente) top-down:

Per confrontare le parole dobbiamo confrontare le lettere:

function z = strcmp(p1, p2)
  z = 0; % assumo che siano uguali
  for ii = 1:length(p1)
    <confronto le lettere in posizione ii>
  end
end

Un Esempio: Confronto Di Parole

Approccio (tendenzialmente) top-down:

Le lettere possono essere confrontate direttamente:

function z = strcmp(p1, p2)
  z = 0;
  for ii = 1:length(p1)
    if p1(ii) < p2(ii)
      <gestisci il risultato>
    end
    if p1(ii) > p2(ii)
      <gestisci il risultato>
    end
  end
end

Un Esempio: Confronto Di Parole

Approccio (tendenzialmente) top-down:

A questo punto calcolare il risultato è banale:

function z = strcmp(p1, p2)
  z = 0;
  for ii = 1:length(p1)
    if p1(ii) < p2(ii)
      z = -1
      break % interrompo la computazione!
    end
    if p1(ii) > p2(ii)
      z = 1
      break % interrompo la computazione!
    end
  end
end

Un Esempio: Confronto Di Parole

Approccio (tendenzialmente) bottom-up:

Le stringhe sono vettori di numeri: possiamo confrontarle

function z = strcmp(p1, p2)
  s1 = p1 < p2
  s2 = p1 > p2
end

Se provo ad invocare la funzione ottengo:

strcmp('cane', 'casa') % stampa [0, 0, 1, 0]
                       % stampa [0, 0, 0, 1]

Il risultato dipende da dove (s1 ed s2) si trova l'1 più a sinistra

Un Esempio: Confronto Di Parole

Funzione find

Octave offre la funzione:

find(V) % denota gli indici dei valori ~= 0 in V
find(V, N) % denota i primi N indici di cui sopra

Input:

• Un vettore, oppure un vettore ed un intero

Output:

• Un vettore con gli indici degli elementi non nulli
• Solo i primi N indici, se viene passato un intero

Un Esempio: Confronto Di Parole

Approccio (tendenzialmente) bottom-up:

Posso usare find per trovare la posizione degli 1

function z = strcmp(p1, p2)
  s1 = p1 < p2;
  s2 = p1 > p2;
  n1 = find(s1, 1)
  n2 = find(s2, 1)
end

Se provo ad invocare la funzione ottengo:

strcmp('cane', 'casa') % stampa 3
                       % stampa 4

Un Esempio: Confronto Di Parole

Approccio (tendenzialmente) bottom-up:

La differenza tra n1 ed n2 fornisce il risultato

function z = strcmp(p1, p2)
  s1 = p1 < p2;
  s2 = p1 > p2;
  n1 = find(s1, 1);
  n2 = find(s2, 1);
  z = n1 - n2
end

Se provo ad invocare la funzione ottengo:

strcmp('cane', 'casa') % denota -1 (< 0)

Un Esempio: Confronto Di Parole

Approccio (tendenzialmente) bottom-up:

Aggiungiamo una piccola modifica per gestire stringhe identiche:

function z = strcmp(p1, p2)
  s1 = p1 < p2;
  s2 = p1 > p2;
  n1 = find(s1, 1);
  n2 = find(s2, 1);
  if length(n1) == 0
    z = 0
  else
    z = n1 - n2
  end
end

Top-Down vs Bottom-Up

Il metodo top-down

• Aiuta ad affrontare il problema in modo ordinato (PRO)
• Facilita la verifica di correttezza del programma (PRO)
• Può rendere difficile esaminare i risultati parziali (CON)

Il metodo bottom-up

• È un po' disordinato e non facilita la verifica di correttezza (CON)
• Può essere più veloce, sia da scrivere che da eseguire (PRO)
• Permette facilmente di esaminare i risultati parziali (PRO)

Di fatto, si usano sempre insieme

Elementi di Informatica e
Applicazioni Numeriche T

Costruzione Rapida di Vettori e Matrici

Costruzione Rapida di Vettori e Matrici

Vediamo alcune funzioni per costruire vettori/matrici

Per ottenere una matrice M x N di zeri:

zeros(M, N)

Restituisce una matrice M x N di 1:

ones(M, N)

Per ottenre una matrice M x N di numeri casuali in (0, 1)

rand(M, N)

• Ricorda che un vettore per Octave è una matrice

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio: Prodotto di un Vettore (F)

Esercizio: Prodotto di un Vettore

Octave fornisce una funzione per calcolare il prodotto di un vettore:

prod(X)

Definite una nuova funzione:

XXX_prod(V) % XXX è un qualunque prefisso

• Che calcoli il prodotto di un vettore V, passato come argomento

Qualche dritta:

• La funzione deve essere in un file di nome XXX_prod.m
• Usate rand per ottenere vettori casuali e fare test
• Confrontate i risultati con quelli di prod

Soluzione

Una possibile soluzione:

function yy = ch3_prod(xx)
  yy = 1;
  for v = xx
    yy = yy .* v;
  end
end

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio: Distanza Euclidea (F)

Esercizio: Distanza Euclidea

Octave fornisce una funzione per calcolare la norma di un vettore:

norm(X, P) % usate help per i dettagli

• X è il vettore
• P è l'ordine della norma

Per P = 2, la funzione calcola la distanza euclidea dall'origine:

$$\| x \| = \sqrt{\sum_{i} x_i^2}$$

Esercizio: Distanza Euclidea

Definite una nuova funzione:

XXX_norm(X) % XXX è un qualunque prefisso

• Che calcoli la norma di ordine due del vettore X

Qualche dritta:

• La funzione deve essere in un file di nome ch3_prod.m
• Usate rand per ottenere vettori casuali e fare test
• La radice quadrata si può calcolare con:
  • La funzione sqrt
  • L'elevamento a potenza .^0.5

Soluzione

Una possibile soluzione:

function yy = ch3_norm(xx)
  yy = 0;
  for vv = xx
    yy = yy + vv.^2;
  end
  yy = sqrt(yy);
end

Un'altra possibile soluzione:

function yy = ch3_norm(xx)
  xx2 = xx.^2;
  yy = sqrt(sum(xx2));
end

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio: Argmax (F)

Esercizio: Argmax

Octave permette di trovare il massimo elemento di un vettore con:

max(X)

• La funzione può restituire anche due risultati

Se invocata con due elementi a sinistra dell'operatore "=":

[V, I] = max(X)

La funzione restituisce:

• Il massimo elemento in V
• Il primo indice a cui può essere trovato in I

Così, svolge anche il ruolo della funzione matematica ${\rm argmax}$

Esercizio: Indice del Massimo Elemento

Definite una nuova funzione:

[V, I] = XXX_max(X) % XXX è un qualunque prefisso

Che replica il comportamento di max in Octave, restituendo:

• In V il massimo elemento del vettore X
• In I l'indice della sua prima occorrenza

Per definire una funzione che restituisce più argomenti la sintassi è:

function [<r1>, <r2>, ...] = <nome>(<p1>, <p2>, ...)
    ...
end

Soluzione

Una possibile soluzione:

function [yy, ii] = ch3_max(xx)
  ii = 1;
  yy = xx(1);
  for jj = 2:length(xx)
    if xx(jj) > yy
      yy = xx(jj);
      ii = jj;
    end
  end
end

Una possibile invocazione:

[y1, i1] = ch3_max([1, 7, 3, 2, 5, 10, 9, 7, 10])

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio: Prodotto Scalare (F)

Esercizio: Prodotto Scalare

Octave permette di effettuare il prodotto scalare con:

X * Y' % HP: vettori riga
dot(X, Y) % funzione dedicata

• X e Y sono due vettori della stessa lunghezza

Definite una nuova funzione:

XXX_dot(X, Y) % scegliete il prefisso XXX

Che replichi la stessa funzionalità

• Usare sempre i comandi di Octave per controllare se funziona

Soluzione

Una possibile soluzione:

function zz = ch3_dot(xx, yy)
  zz = 0;
  for ii = 1:length(xx)
    zz = zz + xx(ii) .* yy(ii);
  end
end

Oppure:

function zz = ch3_dot(xx, yy)
  zz = sum(xx .* yy);
end

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio: Elementi Non Nulli (M)

Esercizio: Elementi Non Nulli

Octave fornisce la funzione:

find(X)

• che restituisce gli indici degli elementi diversi da 0

Definite una nuova funzione:

XXX_find(X) % scegliete il prefisso XXX

Che replichi tale funzionalità.

• Usare sempre i comandi di Octave per controllare se funziona

Soluzione

Una possibile soluzione:

function yy = ch3_find(xx)
  yy = [];
  k = 1;
  for ii = 1:length(xx)
    if xx(ii) ~= 0
      yy(k) = ii;
      k = k + 1;
    end
  end
end

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio: Matrice Diagonale (F/D)

Esercizio: Matrice Diagonale

Octave permette di costruire una matrice diagonale con:

diag(X)

• Restituisce una matrice diagonale
• Gli elementi sulla diagonale sono quelli del vettore X

$$\left(\begin{array}{cccc} x_1 & 0 & \ldots & 0 \\ 0 & x_2 & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & x_n \\ \end{array}\right)$$

Esercizio: Matrice Diagonale

Definite una nuova funzione:

XXX_diag(X) % XXX è un qualunque prefisso

Che replichi il comportamento di diag in Octave

Qualche dritta:

• Ridate un'occhiata alla lista di funzioni per costruire vettori/matrici
• Usate la funzione di Octave per controllare la correttezza

Soluzione

Una possibile soluzione:

function yy = ch3_diag(xx)
  nn = length(xx);
  yy = zeros(nn);
  for ii = 1:nn
    yy(ii,ii) = xx(ii);
  end
end

Soluzione

Un'altra possibile soluzione:

function yy = ch3_diag(xx)
  nn = length(xx);
  yy = zeros(nn);
  ii = (0:nn-1) .* nn + (1:nn); % idx sulla diagonale
  yy(ii) = xx; % indicizzazione via vettore unico
end

• Data una matrice con $n$ elementi per colonna
• Dati due indici $i$ e $j$ per le righe e le colonne
• L'indice unico è dato da $(j-1) * n + i$
• Quindi gli indici sulla diagonale hanno forma: $(i-1) * n + i$

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio: Indicizzazione
mediante Vettore (F/M)

Esercizio: Indicizzazione mediante Vettore

Abbiamo visto che Octave permette di accedere ad un vettore con:

V(I)

• V è un vettore
• I è un vettore di indici

Definite una nuova funzione:

XXX_index(V, I)

Che replica la stessa funzionalità

• Usare sempre i comandi di Octave per controllare se funziona

Soluzione

Una possibile soluzione:

function yy = ch3_index(xx, ii)
  nn = length(ii);
  yy = zeros(1, nn);
  for jj = 1:nn
    kk = ii(jj); % Ottengo l'indice in xx
    yy(jj) = xx(kk); % Assegno il valore
  end
end

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio: Indicizzazione
con Valori Logici (M/D)

Esercizio: Indicizzazione con Valori Logici

Abbiamo visto che Octave permette di accedere ad un vettore con:

V(I)

• V è un vettore
• I è un vettore di valori logici

Definite una nuova funzione:

XXX_index2(V, I)

Che replica la stessa funzionalità

• Usare sempre i comandi di Octave per controllare se funziona

Soluzione

Una possibile soluzione:

function yy = ch3_index2(xx, cc)
  yy = [];
  kk = 1; % Indice corrente sul vettore risultato
  for jj = 1:length(xx)
    if cc(jj) ~= 0
      yy(kk) = xx(jj); % Assegno un elemento
      kk = kk + 1; % Incremento l'indice
    end
  end
end

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio: Elementi Distinti (D)

Esercizio: Elementi Distinti

Octave fornisce la funzione:

unique(X)

• X che restituisce gli elementi distinti del vettore X

Definite una nuova funzione:

XXX_unique(X, Y) % scegliete il prefisso XXX

Che replichi la stessa funzionalità

• Octave ordina anche l'array di uscita: noi non lo faremo
• Usare sempre i comandi di Octave per controllare se funziona

Soluzione

Una possibile soluzione:

function yy = ch3_unique(xx)
  yy = []; % Uso vettore vuoto
  ii = 1; % Indice corrente sul vettore risultato
  for vv = xx
    % Controllo se l'elemento non sia già presente
    if ~any(yy == vv)
      yy(ii) = vv; % Inserisco l'elemento
      ii = ii + 1; % Incremento l'indice
    end
  end
end

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio: Identificazione
di Numeri Primi (D)

Esercizio: Identificazione di Numeri Primi

Octave fornisce la funzione:

isprime(N)

• che individua se il numero N è primo

Definite una nuova funzione:

XXX_isprime(N) % scegliete il prefisso XXX

Che replichi tale funzionalità

• Un numero è primo se è divisibile sono per 1 e per se stesso
• Si intende: divisibile secondo la divisione intera

Esercizio: Identificazione di Numeri Primi

Octave permette di calcolare la divisione intera con:

idivide(x, y)

E il resto della divisione intera con:

mod(x, y)

Esempio:

idivide(5, 2) % denota 2
mod(5, 2) % denota 1

x è divisibile per y sse il resto è 0

Soluzione

Una possibile soluzione:

function yy = ch3_isprime(vv)
  yy = true; % assumo che il numero sia primo
  for ww = 2:sqrt(vv) % Cerco un divisore
    if mod(vv, ww) == 0 % verifico il resto
      yy = false % il numero non è primo
      break % posso terminare
    end
  end
end

Possiamo smettere di cercare divisori quando arriviamo a $\sqrt{v}$

• Se $v$ è divisibile per un numero $> \sqrt{v}$...
• ...Allora è anche divisibile per un numero $\leq \sqrt{v}$