Esercizio 1

Si progetti una pista da moto-cross con la forma data:

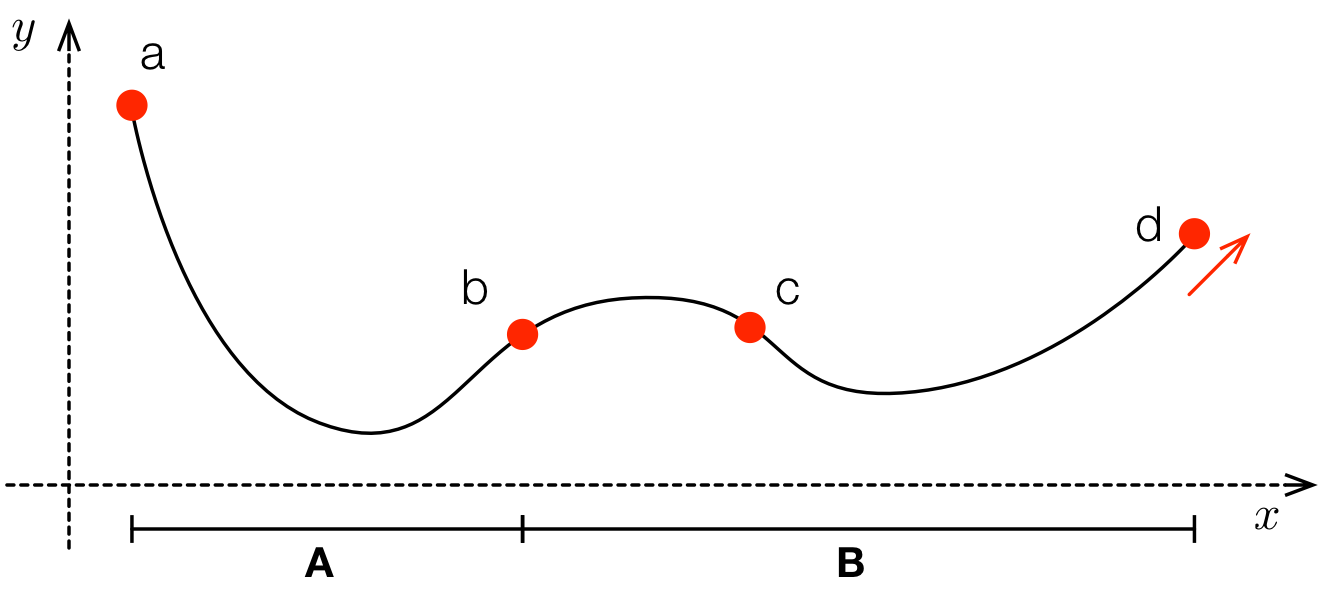
• Il tratto è descritto da due curve polinomiali, A e B
• La curva A deve passare per i punti $a, b$
• La curva B deve passare per i punti $b, c, d$

Esercizio 1

Si progetti una pista da moto-cross con la forma data:

• I punti $a, b, c, d$ hanno coordinate $x, y$ note
• La pendenza in $d$ deve essere di 45°
• La pendenza non deve avere discontinuità in $b$

Esercizio 1

Si considerino i seguenti problemi:

• Q1: Come si possono ottenere le due equazioni del circuito?
• Q2: Come si può calcolare l'area sotto la curva?
  • Essa potrebbe rappresentare (e.g.) la quanità di materiale...
  • ...Necessaria per costruire la pista
  • Si assuma che tutta la curva sia al di sopra dell'asse delle $x$
• Q3: Come calcolare la quota minima raggiunta?

NOTA: questo esercizio è mediamente facile...

Soluzione (Q1)

• Si tratta di definire i parametri di due curve polnomiali $f_\beta(x), g_\beta(x)$
• Le due curve devono soddisfare le equazioni:

$$\begin{align} & f_\beta(x_a) = y_a & & f_\beta(x_b) = y_b & & f'_\beta(x_b) = g'_\beta(x_b) \\ & g_\beta(x_b) = y_b & & g_\beta(x_c) = y_c & & g_\beta(x_d) = y_d & g'_\beta(x_d) = 1 \end{align}$$

È un sistema con 7 equazioni, quindi ci vogliono 7 coefficienti

• $g_\beta(x)$ è coinvolta singolarmente in 4 equazioni, quindi $n_g = 3$
• Di conseguenza abbiamo $n_f = 2$

NOTA: una equazione coinvolge sia $f_\beta(x)$ che $g_\beta(x)$

• Per questa ragione, ho un sistema unico anziché due sistemi

Soluzione (Q1)

Le due funzioni $f_\beta(x), g_\beta(x)$ sono date da:

$$\begin{align} & f_\beta(x) = \beta_1 x^2 + \beta_2 x^1 + \beta_3 \\ & f'_\beta(x) = 2 \beta_1 x + \beta_2 \\ & g_\beta(x) = \beta_4 x^3 + \beta_5 x^2 + \beta_6 x + \beta_7 \\ & g'_\beta(x) = 3 \beta_4 x^2 + 2 \beta_5 x + \beta_6 \end{align}$$

• I parametri si possono trovare risolvendo il sistema precedente
• Il sistema è lineare in $\beta$: si può utilizzare (e.g.) la riduzione di Gauss
• In Octave, possiamo utilizzare la divisione sinistra

NOTA: di seguito, i parametri $\beta$ verranno omessi nella notazione

Soluzione (Q2)

Per rispondere al quesito due è sufficiente integrare le due funzioni:

• Siano $Q_A$ e $Q_B$ le aree sotto le curve A e B

$$\begin{align} & Q_A = \int_{x_a}^{x_b} f(x)\, dx \\ & Q_B = \int_{x_b}^{x_d} g(x)\, dx \\ \end{align}$$

• L'area totale è data quindi da $Q = Q_A + Q_B$

Soluzione (Q3)

Per rispondere a Q3, vanno confrontati i minimi delle due curve

La prima curva ha un unico punto stazionario:

• Esso rappresenta un minimo
• Lo si può individuare risolvendo:

$$f'(x) = 2 \beta_1 x + \beta_2 = 0$$

• L'equazione si può risolvere anche per via analitica
• La soluzione è data da $x^*_A = - \frac{1}{2}\frac{\beta_2}{\beta_1}$

Soluzione (Q3)

La seconda curva ha due punti stazionari

• Si possono individuare risolvendo:

$$g'(x) = 3 \beta_4 x^2 + 2 \beta_5 x + \beta_6 = 0$$

Si può risolvere per via analitica o numerica

• Per esempio, possiamo usare il metodo della bisezione
• La forma della curva è approssimativamente nota...
• ...E possiamo notare che c'è un minimo tra $x_c$ e $x_d$
• Quindi possiamo usare $x_c, x_d$ come estremi iniziali per il metodo

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio 2 (modellazione)

Esercizio 2

La forza di attrito aerodinamico è data da:

$$F = \frac{1}{2}\rho v^2 C_D A$$

Dove:

• $\rho$ è la densità del fluido in cui ci si muove
• $v$ è la velocità
• $C_D$ è un coefficiente di attrito
• $A$ è l'area frontale

Esercizio 2

Sono stati fatti $n$ esperimenti su un ciclista professionista:

• Per vari valori di velocità $v_i$ è stata misurata la forza di attrito $F_i$

Esercizio 2

Durante una gara, sono state fatte $m$ misurazioni ad intervalli di $5\, s$

• Ogni misurazione comprende il valore della velocità $w_k$...
• ...E la strada percorsa $x_k$

NOTA: quando la velocità è alta, ovviamente si fa più strada

Esercizio 2

Si considerino i seguenti problemi:

• Q1: Come stimare il valore del prodotto $C_D\, A$ per il ciclista?
  • Si assuma che la densità dell'aria $\rho$ sia nota
• Q2: Come calcolare il lavoro (fisico) svolto dal ciclista in gara?
  • Si ricordi che il lavoro è data dal prodotto forza-spostamento...
  • E che per avanzare bisogna bilanciare la forza di attrito
• Q3: Se si potesse ridurre del 10% il prodotto $C_D\, A$...
  • Come varierebbe il lavoro svolto dal ciclista in gara?
  • Ipotesi: la forza del ciclista rimane invariata
  • Ipotesi: la velocità è costante tra le misurazioni, $\Delta x = w_k \Delta t$

NOTA: questo esercizio è un po' particolare e non facile

Soluzione (Q1)

Per rispondere a Q1 possiamo usare il metodo dei minimi quadrati

• Chiamiamo $\alpha$ il prodotto $C_D\,A$. La funzione approssimante è:

$$f_\alpha(v) = \frac{1}{2}\rho v^2 \alpha$$

• Quindi, per risolvere il problema definiamo una matrice $\Phi$:

$$\Phi = \left(\begin{array}{c} \frac{1}{2}\rho v_1^2 \\ \frac{1}{2}\rho v_2^2 \\ \vdots \end{array}\right)$$

• Quindi troviamo $\alpha$ risolvendo $\Phi^T\Phi \alpha = \Phi^T F$

Soluzione (Q2)

Per rispondere a Q2, dobbiamo:

• Associare ad ogni misurazione un valore di forza
• Sommare il lavoro svolto tra ogni coppia di misurazioni

La forza necessaria per avanzare deve bilanciare quella di attrito

• Quindi ad ogni misurazione di gara $k$ associamo una forza:

$$F_k = \frac{1}{2}\rho w_k^2 \alpha$$

• Dove $\alpha$ è valore determinato per Q1
• La notazione è stessa della forza di attrito (le due sono uguali)

Soluzione (Q2)

• Otteniamo così un vettore di valori di forza $F$...
• Associato al vettore di posizioni misurate $x$

Il lavoro è così data dall'integrale della forza sullo spostamento

• Possiamo calcolarlo a partire dai vettori $F$ e $x$...
• ...Utilizzando il metodo dei trapezi
• Formalmente, abbiamo:

$$E = \sum_{k = 1}^{m-1} \frac{1}{2}(x_{k+1} - x_k) (F_{k+1} + F_k)$$

Soluzione (Q3)

Per rispondere a Q3, occorre simulare gli effetti della modifica di $\alpha$

• Le forze del ciclista sono le stesse (i valori $F_k$ di Q2)
• Vanno però aggiornati i valori di velocità
• Possiamo ottenere i nuovi valori (siano essi $w'_k$) risolvendo:

$$F_k = \frac{1}{2}\rho {w'_k}^2 \frac{9}{10} \alpha$$

• E quindi:

$$w'_k = \sqrt{2 \frac{1}{\rho} \frac{10}{9} \alpha F_k}$$

Soluzione (Q3)

Con l'ipotesi di velocità costante, possiamo ricalcolare gli spostamenti

• Durante ogni intervallo $k$ (lungo 5 secondi)...
• ...Lo spostamento è dato da:

$$\Delta x = (x_{k+1} - x_k) = w'_k \Delta t = 5 w'_k$$

• Quindi sostituendo nella formula del metodo dei trapezi:

$$E' = \sum_{k = 1}^{m-1} \frac{1}{2} 5 w'_k (F_{k+1} + F_k)$$

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio 3 (Modellazione)

Esercizio 3

Un palla di gomma è posta su un percorso con salite e discese

• Il tratto si compone di due curve polinomiali note A e B:

$$\begin{align} & \phi_A(x) = \alpha_1 x^2 + \alpha_2 x + \alpha_3 & & \phi_B(x) = \beta_1 x^3 + \beta_2 x^2 + \beta_3 x + \beta_4 \end{align}$$

Esercizio 3

Un palla di gomma è posta su un percorso con salite e discese

• La curva A va dal punto $x_a$ al punto $x_b$
• La curva B va dal punto $x_b$ al punto $x_c$

Esercizio 3

Un palla di gomma è posta su un percorso con salite e discese

• La palla è originariamente nel punto $x_a$
• La palla è soggetta alla forza di gravità
• La palla ha massa $M$ nota

Esercizio 3

Si considerino i seguenti problemi:

• Q1: Assumendo che la palla non sia soggetta ad altre forze...
  • ...Come determinare l'andamento della posizione delle palla?
  • NOTA: si richiedono ambedue le coordinate della posizione
• Q2: Assumendo che la palla, finché è in moto, sia soggetta...
  • ...Ad un attrito costante $F_r$ nella direzione della tangente...
  • ...Dove si ferma la palla?
• Q3: Come determinare quanta strada fa la palla prima di fermarsi?

NOTE:

• Il fatto che l'attrito sia tangenziale è una facilitazione
• Questo esercizio e difficile

Soluzione (Q1)

Le equazioni delle due curve sono note, quindi;

• Se la coordinata $x$ della posizione della palla è nota...
• ...La coordinata $y$ si può calcolare facilmente:

$$y = \phi(x) = \left\{\begin{aligned} & \phi_A(x) && \text{ se } x \leq x_b \\ & \phi_B(x) && \text{ altrimenti} \end{aligned}\right.$$

Quindi ci basta determinare l'andamento di $x$

• La passa costituisce un sistema dinamico
• Quindi possiamo determinare l'andamento della posizione...
• ...Risolvendo un sistema di equazioni differenziali

Soluzione (Q1)

• Descriviamo lo stato con la posizione $x$ e la velocità tangenziale $v$
• Il sistema di EDO che ne consegue è dato da:

$$\begin{align} & \dot{x} = v \frac{1}{\sqrt{1 + \phi'(x)^2}} \\ & \dot{v} = - g \frac{\phi'(x)}{\sqrt{1 + \phi'(x)^2}} \\ & \text{con: } \phi'(x) = \left\{\begin{aligned} & \phi'_A(x) && \text{ se } x \leq x_b \\ & \phi'_B(x) && \text{ altrimenti} \end{aligned}\right. \end{align}$$

• $\dot{x}$ è dato dalla proiezione sull'asse $x$ della velocità tangenziale
• $\dot{v}$ è dato dalla proiezione sulla tangente di $g$

Soluzione (Q1)

Di fatto, si tratta della EDO che abbiamo visto diverse volte a lezione

• l'unica differenza è che il calcolo delle proiezioni...
• ...è diverso per le due curve A e B

Può essere risolta per esempio con il metodo di Eulero

• Dato un vettore $t$ di istanti di tempo $t_k$...
• ...La soluzione delle EDO sono i vettori $x(t_k)$ e $v(t_k)$

Il vettore $x(t_k)$ risponde a Q1

Soluzione (Q2)

Per rispondere a Q2 dobbiamo incorporare $F_r$ nella EDO:

$$\begin{align} & \dot{x} = v \frac{1}{\sqrt{1 + \phi'(x)^2}} \\ & \dot{v} = - g \frac{\phi'(x)}{\sqrt{1 + \phi'(x)^2}} - \frac{1}{M}\hat{F}_r\\ & \text{con: } \hat{F}_r = \left\{\begin{aligned} & F_r && \text{ se } v > 0 \\ & - F_r && \text{ se } v < 0 \\ & 0 && \text{ altrimenti} \end{aligned}\right. \end{align}$$

• $\phi'(x)$ è definito come nel caso precedente

Soluzione (Q2)

L'EDO si può risolvere di nuovo con il metodo di Eulero

• La soluzione sono i due vettori $x(t_k)$ e $v(t_k)$

A questo punto, sfruttando l'interpolazione lineare di $x(t_k)$ e $v(t_k)$:

• Identifichiamo un istante di tempo $t^*$ tale che:
  • $v(t^*) \simeq 0$, i.e. la velocità è nulla
  • $\dot{v}(t^*) \simeq 0$, i.e. l'accelerazione è nulla
  • $\dot{v}(t^*)$ si può calcolare con l'espressione usata per l'EDO
  • La palla si ferma se sia la velocità che l'accelerazione sono nulle
  • NOTA: la lezione registrata contiene un errore in questo punto
• Il valore di $x(t^*)$ risponde a Q2

Soluzione (Q3)

• Se la palla andasse sempre in avanti (da sx verso dx)
• Allora la strada percorsa sarebbe data da:

$$L = \int_{x_a}^{x(t^*)} \sqrt{1 + \phi'(x)^2}\, dx$$

Purtroppo però la palla può anche tornare indietro

• Quando la palla si muove da dx verso sx...
• ...Sta ancora percorrendo della strada

Come tenerne conto?

Soluzione (Q3)

Una possibile soluzione: sfruttiamo il vettore $x(t_k)$

• Quando ci spostiamo da $x(t_k)$ a $x(t_{k+1})$...
• La lunghezza del tratto di curva percorso è approssimativamente:

$$\sqrt{(x(t_{k+1}) - x(t_k))^2 + (y(t_{k+1}) - y(t_k))^2}$$

• Dove $y(t_k) = \phi(x(t_k))$

Quindi la strada percorsa è data da:

$$L = \sum_{k = 1}^{n-1} \sqrt{(x(t_{k+1}) - x(t_k))^2 + (y(t_{k+1}) - y(t_k))^2}$$

• Dove $n$ è il numero di elementi nel vettore $t$

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio 4 (Analisi)

Esercizio 4

Si consideri lo script seguente:

function y = f(x)
    t = x(end:-1:1);
    y = x + t;
end

x = f([1, 2, 3, 4])
t = (x == 5)

• Che cosa stampa?
• Si motivi (intuitivamente) la risposta

Soluzione

function y = f(x)
    t = x(end:-1:1); % t è x, in ordine invertito
    y = x + t;
end

% f([1,2,4,4]) restituisce [1,2,4,4] + [4,4,2,1]
% Quindi viene stampato: [5, 6, 6, 5]
x = f([1, 2, 4, 4])
% (x == 5) restituisce un vettore, che contiene il valore
% per le posizioni in x che soddisfano l'uguaglianza
% Quindi viene stampato: [1, 0, 0, 1]
t = (x == 5)

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio 5 (Analisi)

Esercizio 5

Si consideri lo script seguente:

function y = f(x, v)
    t = x(x <= v);
    y = sum(t);
end

M = [1, 2, 1, 3, 1, 3];
f(M, 1)
f(M, 2)

• Che cosa stampa?
• Si motivi (intuitivamente) la risposta

Soluzione

function y = f(x, v)
    % Se x = [1,2,1,3,1,3] e v è 2
    % Allora (x <= v) è [1,1,1,0,1,0]
    % E x(x <= v) è [1,2,1,1]
    t = x(x <= v);
    y = sum(t);
end

M = [1, 2, 1, 3, 1, 3];
f(M, 1) % Stampa sum([1,1,1]), quindi 3
f(M, 2) % Stampa sum([1,2,1,1]), quindi 5

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio 6 (codifica)

Esercizio 6

Si codifichi la funzione:

function x = midpoint(f, x0, t)

Che risolve una EDO con il metodo del punto intermedio

• f è una funzione che calcola la derivata dello stato corrente:

  function  dx = f(x, t)
  

  • x è lo stato (uno scalare), t è l'istante di tempo corrente
• x0 è il valore iniziale dello stato (uno scalare)
• t è il vettore dei tempi per cui va determinato lo stato

Si discuta brevemente il metodo

Soluzione

Il metodo del punto intermedio risolve una EDO in base all'iterazione:

$$\begin{align} & x^{(k+1)} = x^{(k)} + (t^{(k+1)} - t^{(k)})\, f(x_m^{(k)}, t_m^{(k)}) \\ \text{con: } & t_m^{(k)} = \frac{1}{2} (t^{(k+1)} + t^{(k)}) \\ \text{e: } & x_m^{(k)} = x^{(k)} + (t_m^{(k+1)} - t^{(k)})\, f(x^{(k)}, t^{(k)}) \end{align}$$

• $t_m^{(k)}$ è l'istante di tempo a metà tra $t^{(k)}$ e $t^{(k+1)}$
• $x_m^{(k)}$ è il corrispondente valore dello stato
• $x_m^{(k)}$ viene approssimato con il metodo di Eulero
• $f(x_m^{(k)}, t_m^{(k)})$ è la derivata dello stato nel punto intermedio

Soluzione

Una possibile codifica:

function x = midpoint(f, x0, t)
    x(1) = x0;
    for ii = 1:length(t)-1
        tm = t(ii+1) + t(ii); % Punto intermedio
        df = f(x(ii), t(ii)); % Derivata in t(ii)
        % Ora ottengo lo stato nel punto intermedio
        xm = x(ii) + (tm - t(ii)) .* df;
        % Prossimo stato
        dt = t(ii+1) - t(ii);
        x(ii+1) = x(ii) + dt .* f(xm, tm);
    end
end