Esercizio 1

Un serbatoio atmosferico contenente un reagente chimico...

...Viene svuotato attraverso una condotta e riempito con una pompa

Il serbatoio è posto ad $1\,m$ di altezza ed ha un raggio di $50\,cm$
Il serbatoio ha un livello iniziale di $2\,m$
Il reagente ha $\rho = 1.189\times 10^3$ e $\mu = 2.100\times 10^{-3}$
La condotta ha $5\, cm$ di diametro, scabrezza $2\, mm$ ed è lunga $30\,m$
Per le perdite dovute all'imbocco della condotta si consideri $k = 0.5$
La pompa immette reagente con una portata data da:

$Q_{in} = Q_{max} \left(1 + \sin\left(2\pi \frac{t}{240}\right)\right)$

Con $Q_{max} = 0.001$

Esercizio 1

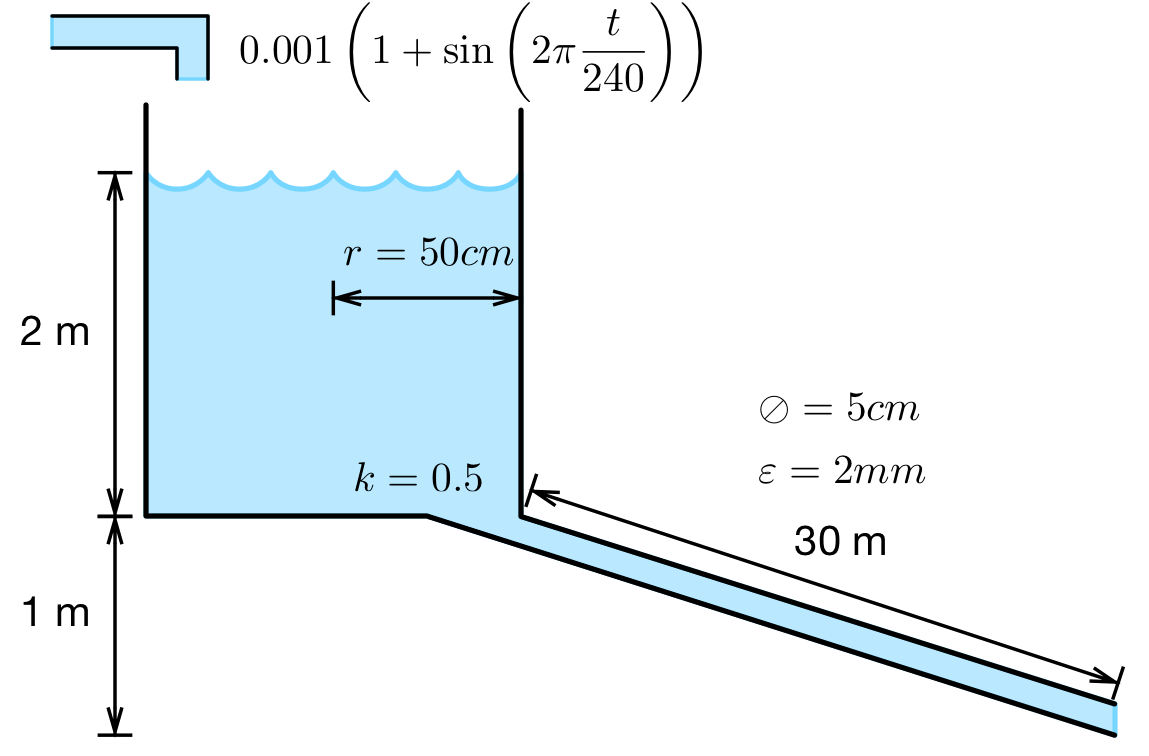
Si determini se il livello di reagente tende a calare o crescere

Si programmi a partire da uno script che calcola la portata iniziale

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio 2

Si consideri il serbatoio dell'esercizio 1:

Partire da una copia dello script utilizzato per risolverlo:

Q1: Si definisca (nello script) una funzione:
```
function DeltaH = DeltaH_in_240_sec(Qmax)
```
- Che calcola la differenza tra il volume iniziale di reagente...
- ...ed il volume dopo 240 secondi
Q2: Si utilizzi la funzione per determinare il valore di $Q_{max}$ ...
- ...Che stabilizza il livello del serbatoio nel lungo periodo
Q3 (opzionale): Si verifichi che il valore di $Q_{max}$ sia corretto

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio 3

Si deve posizionare una pompa su una condotta:

La pompa deve servire due utenze
La prima utenza si trova a $1322\,m$ dalla condotta
La seconda utenza si trova a $2131\,m$ dalla condotta
La seconda utenza è $1\,Km$ a valle della prima

Le due utenze verranno servite:

Costruendo delle condotte rettilinee...
...Che connettono la pompa alle utenze

Esercizio 3

Q1: Si definisca una funzione:
```
function d = dist(a)
```
- Che calcoli la lunghezza totale delle due condotte...
- ...A partire dalla posizione a della pompa

Esercizio 3

Q2: Si disegni l'andamento di dist(a) in funzione di a
Q3: Si determini il valore di a che minimizza dist(a)
- Si individuino i punti stazionari risolvendo $dist'(a) = 0$
- A tal fine, si definisca la funzione:
```
function dd = ddist1(a)
```
- Che calcoli la derivata di dist per via analitica

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio 4

Si consideri la situazione dell'esercizio 3

A partire da una copia dello script utilizzato per risolverlo:

Q1: Si determini il valore di a che minimizza dist(a)
- Si individuino i punti stazionari risolvendo $dist'(a) = 0$
- A tal fine, si definisca la funzione:
```
function dd = ddist2(a)
```
- Che calcoli la derivata di dist(a) per approssimazione numerica
- Si utilizzi l'approssimazione basata sul rapporto incrementale

Esercizio 4

OSSERVAZIONE:

Utilizzando una approssimazione numerica per la derivata...
...Si evita di derivarne al forma analitica

In alcuni casi, la derivata analitica non può essere ottenuta!

ATTENZIONE:

Si calibri il valore del passo "infinitesimo" del rapporto incrementale...
...In modo da ottenere il risultato corretto

Che ordine di grandezza è necessario? Per quali ragioni?

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio 5

Due serbatoio atmosferici contenenti acqua sono collegati:

Il primo serbatoio ha raggio $40\,cm$ , il secondo $80\,cm$
Il primo serbatoio ha un livello di $3\,m$ , il secondo di $30\,cm$
La condotta ha un diametro di $8\,cm$ ed è lunga $20\,m$
La scabrezza della condotta è di $2\,mm$
Per le perdite dovute all'imbocco, si consideri $k = 0.5$
Per le perdite dovute allo sbocco, si consideri $k = 1$

È dato uno script che calcola la portata iniziale della condotta

Lo si utilizzi come partenza per programmare

Esercizio 5

Q1: Disegnare l'andamento dei due livelli
Q2: Determinare il livello finale dei due serbatoi
Q3: Determinare il livello iniziale del primo serbatoio...
- ...Perché si arrivi all'equilibrio in $200\,s$
- NOTA: la quantità d'acqua è fissa, quindi anche il livello finale

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio 6

Si vuole determinare e caratterizzare una curva parabolica

La curva deve passare per il punto $(x_0, y_0) = (0, 5)$
La curva deve avere un minimo in $(x_1, y_1) = (3, 0)$

Q1: Si definisca una funzione che determini i coefficienti della parabola:

function p = find_curve()

Si disegni poi la curva nell'intervallo $[x_0, x_2] = [0, 5]$
Si determini il valore di $y$ per $x = x_2 = 5$

Q2: Si determini la lunghezza della parabola

Si utilizzi il metodo visto a lezione basato sull'integrazione

Elementi di Informatica e
Applicazioni Numeriche T

Esercizio 7

Si consideri la curva parabolica dell'esercizio 6:

Si assuma di poter decidere la la posizione di $x_1$ ...
...Ossia del punto in cui la parabola raggiunge un minimo

Partendo da una copia dello script utilizzato per l'esercizio 6:

Q1: Si definisca una funzione:
```
function area = curve_area(x1)
```
- Che calcoli l'area sotto la parabola nell'intervallo $[0,5]$
- La funzione dovrà ri-determinare i coefficienti della parabola!
- Si sfruttino (modificandole) le funzione introdotte per l'es6

Esercizio 7

Q2: Si determini la posizione di $x_1$ ...
- ...Che minimizza l'area sotto la parabola
- Si noti che si tratta di un problema di ottimizzazione...
- ...Che richiederà di calcolare la derivata dell'area sotto la parabola

SUGGERIMENTO: Per ottenere la derivata dell'area

Si utilizzi una approssimazione numerica
Per esempio, quella basata sul rapporto incrementale
Si calibri il valore del passo infinitesimo in modo opportuno

# Questa lezione Parabola che passa per due punti fissi ed ha un minimo fissato Q1: definire una funzione che calcoli l'area, a seconda della posizione del secondo punto Q2: posizionare il secondo punto in modo da minimizzare l'area # Prossime lezioni Determinazione dello stato stazionario - Utilizzando il metodo del punto intermedio macchina su traiettoria # Esercizi Dove si ferma la palla? Palla lanciata con una certa velocità Soggetta a: trascinamento + attrito volvente Macchina su traiettoria Circuito elettrico? # Remeber to explain: array concatenation memorizzazione delle matrici in memoria continue (magari nella lezione sull'ottimizzazione) trattamento degli argomenti non specificati Gestione errori (error/warning) Debugging I/O semplice + disp + printf? Per stampare con precisione alta # Possibili esercizi: determinant computation (recursive!) factorial computation (recursive!) matrix argument to vector operation - a good occasion to explain multiple functions in a single file sieve of erathostenes other algorithms to find prime numbers? permutations - Permute vectors - Permute rows/columns of a matrix Taylor series expansion? convolution? bubble sort / naive sort comparison functions set operations - intersection - union - substract? - powerset? continued fraction expansion Coordinate conversion (cartesian, polar) Some matrix factorizations/decompositions? - Choleski - LU decomposition - QR factorization - Singular Value Decomposition Gradient descent Newton method Fixed point iteration Bisection method - bracket a zero - convex optimization Minimization by repeated evaluation Golden section search Numeric gradient/Jacobian/Hessian Nelder-Mead? RNG algorithms (something simple) Using diagonal matrices for scaling Integration methods: - Numerical integration based on Gaussian quadrature. - Numerical integration using an adaptive vectorized Simpson’s rule. - Numerical integration using an adaptive Lobatto rule. - Numerical integration using an adaptive Gauss-Konrod rule. - Numerical integration using adaptive Clenshaw-Curtis rules. - Numerical integration of data using the trapezoidal method. Multi-dimensional integration? - Recursive appraoch - Orthogonal collocation ODE - algo? - reduction to first order Optimization? - LP, QP (null-space active-set method)... the algos are too complex - QP: basic method for convex problems? Zero-gradient - NLP via sequential quadratic programming - Least Square method? Descriptive statistics - Mean - Median - Variance - Stdev (second moment, statistic bias -- maybe this one later) - Mode? - Quartiles, quantiles - Explain histograms, too? - Histogram count computation - correlation/covariance? "True" statistics & probability theory - stat plots - unbiased estimators - some probability distributions - central limit theorem - Distributions - pdf, cdf, quantiles - One or two stat tests? - Confidence intervals? Generate permutations? Centering / Normalization Polynomials - Representation? - Horner's method? - Roots of a polynomial: Frobenius companion matrix, eigenavalues - poles? Interpolation - Nope - Use variable transformation for power law fitting Verifica stato di un elemento di un array Sort by argument Calcolo della radice quadrata Serie di Taylor (per calcolare una funzione) Goal: algoritmi + complessi ed esempi di propagazione degli errori valutazione di un polinomio (trivial) valutazione di un polinomio (Horner) Somme: - Somma "normale" - Somma gerarchica - Somma di Kahan Numeri interi - identificazione di numeri primi - fattorizzazione in numeri primi (trial division) Algoritmi di ordinamento: - Solo naive sort e bubble sort RNG - un algoritmo semplice - esempi di utilizzo di RNG in Octave Valutazione di una funzione a gradini - Lookup in una tabella chiave-valore - Valutazione in punti multipli Numeri interi ed algoritmi - Interi in Octaves - Promozione/demozione? - sieve of erathostenes (magari nella lezione 3) - fattorizzazione in numeri primi (trial division) - GCD GCD: q = gcd a = n_a q // q è il GCD di a e b b = n_b q // q è il GCD di a e b a = p b + r // divisione di a per b Quindi: n_a q = a = p b + r = p n_b q + r Quindi n_a = p n_b + r / q Deve venire un intero => r/q deve essere intero => r è divisibile per q * Si dovrebbe poter fare lo stesso ragionamento anche per la sottrazione

Elementi di Informatica e Applicazioni Numeriche T

Esercizio 1

Elementi di Informatica e
Applicazioni Numeriche T