Elementi di Informatica e
Applicazioni Numeriche T
Interpolazione ed Estrapolazione
Esempio: Profilo di Velocità di un Fluido
Consideriamo un problema realistico
- Dato un fluido che scorre in una condotta di diametro
15cm... - ...Vogliamo determinarne sperimentalmente il profilo di velocità
Metodo:
Utilizziamo un sensore per effettuare una serie di misurazioni
- Ogni misurazione
iè nella forma(xi,yi) xiè la posizione del sensoreyiè la velocità misurata
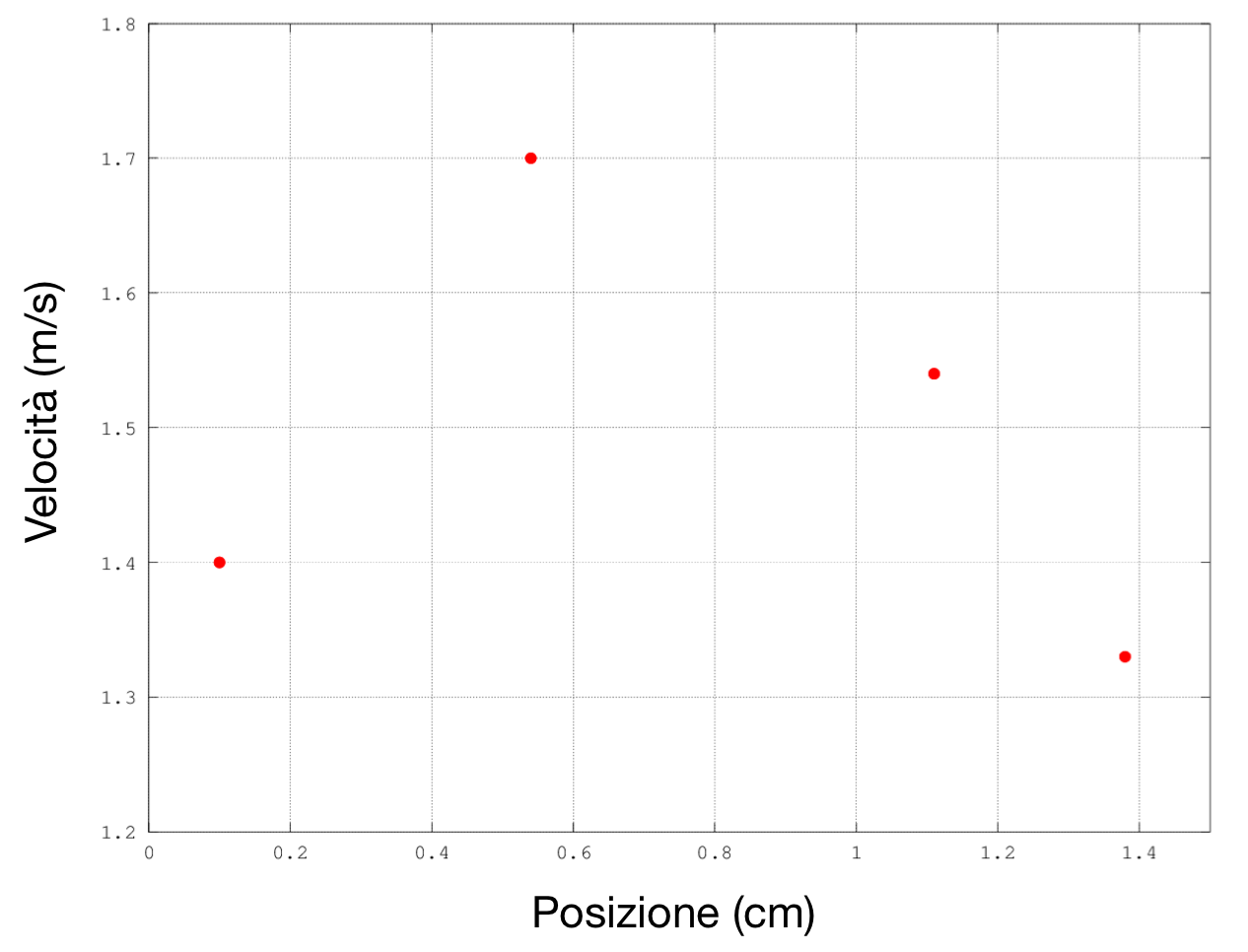
Possiamo disegnare la misurazioni su un piano cartesiano...
Esempio: Profilo di Velocità di un Fluido
Esempio: Velocità di Reazione
Un secondo problema
- Determinare come la velocità di una reazione chimica...
- ...dipende dalla temperatura a cui essa avviene
Metodo:
Effettuiamo una serie di esperimenti. Per ogni esperimento i:
- Variamo la temperatura
xiin modo regolare - Misuriamo la velocità di reazione
yi
Possiamo di nuovo disegnare la misurazioni...
Esempio: Velocità di Reazione

Interpolazione/Estrapolazione
Abbiamo le informazioni che ci interessano per alcuni punti
Ma come facciamo a conoscere la velocità in ogni punto?
Interpolazione/Estrapolazione
Abbiamo le informazioni che ci interessano per alcuni punti
Ma come facciamo a conoscere la velocità in ogni punto?
Approccio 1: misuriamo la velocità in ogni punto
- Ovviamente, questo approccio non è pratico
Interpolazione/Estrapolazione
Abbiamo le informazioni che ci interessano per alcuni punti
Ma come facciamo a conoscere la velocità in ogni punto?
Approccio 1: misuriamo la velocità in ogni punto
- Ovviamente, questo approccio non è pratico
Approccio 2: inferiamo la velocità
- Nei punti intermedi
- Prima e dopo le posizioni estreme
I due problemi si chiamano interpolazione ed estrapolazione
Interpolazione/Estrapolazione

Interpolazione/Estrapolazione

Elementi di Informatica e
Applicazioni Numeriche T
Polinomio Interpolante
Funzione Interpolante
Proviamo ad impostare formalmente il problema:
- Data una serie di
mdi punti(xi,yi) - HP: i punti sono distinti (i.e. xi≠xj ∀i≠j)
- Vogliamo determinare una funzione
f(x)tale che:
f(xi)=yi∀i=1..m
Se ci riusciamo, abbiamo risolto tutti i nostri problemi:
- Possiamo valutare
f(x)conxi<x<xj(interpolazione) - E possiamo estrapolare i dati nello stesso modo
Grossa difficoltà: come deve essere fatta f(x)?
Polinomio Interpolante
Vediamo cosa succede se f(x) è un polinomio di grado n
In questo caso, abbiamo che:
f(x)=n∑j=0βjxj
Polinomio Interpolante
Vediamo cosa succede se f(x) è un polinomio di grado n
In questo caso, abbiamo che:
f(x)=n∑j=0βjxj
Per ogni punto i, la funzione deve soddisfare:
f(xi)=n∑j=0βjxji=yi
- Le incognite sono i coefficienti
βj! - Quindi le equazioni sono lineari
Polinomio Interpolante
Possiamo quindi usare la forma matriciale:
(xn1xn−11…x111xn2xn−12…x121⋮⋮⋱⋮⋮xnm−1xn−1m−1…x1m−11xnmxn−1m…x1m1)(βnβn−1…β1β0)=(ymym−1…y2y1)
La matrice V a sx è nota come matrice di Vandermonde
- Ogni riga si riferisce ad un punto
i - La riga contiene
xi, elevato a tutte la potenze
Proprietà: V è non singolare (perché i valori di xi sono distinti)
Polinomio Interpolante
Possiamo quindi usare la forma matriciale:
(xn1xn−11…x111xn2xn−12…x121⋮⋮⋱⋮⋮xnm−1xn−1m−1…x1m−11xnmxn−1m…x1m1)(βnβn−1…β1β0)=(ymym−1…y2y1)
Se abbiamo n>m−1 (più termini nel polinomio che punti):
- Il sistema è sottodeterminato
- Ci sono molte soluzioni possibili
- A noi basterebbe trovarne una, però...
Polinomio Interpolante
Possiamo quindi usare la forma matriciale:
(xn1xn−11…x111xn2xn−12…x121⋮⋮⋱⋮⋮xnm−1xn−1m−1…x1m−11xnmxn−1m…x1m1)(βnβn−1…β1β0)=(ymym−1…y2y1)
Se invece n=m−1 (tanti punti quanti termini del polinomio):
- Esiste una sola soluzione, quindi un solo polinomio interpolante
- Per due punti passa una sola retta, per tre punti una sola parabola...
Esempio: Profilo di Velocità di un Fluido
Vediamo un esempio numerico:
Supponiamo di avere i seguenti punti per il nostro fluido in condotta:
xi (m) |
yi (m/s) |
|---|---|
0.010 |
1.40 |
0.054 |
1.70 |
0.111 |
1.54 |
0.138 |
1.33 |
Dobbiamo risolvere il sistema:
Vβ=y
Esempio: Profilo di Velocità di un Fluido
Vediamo un esempio numerico:
La matrice di Vandermonde è:
x3ix2ix1ix0iV=(0.00100000.01000000.10000001.00000000.15746400.29160000.54000001.00000001.36763101.23210001.11000001.00000002.62807201.90440001.38000001.0000000)
Risolvendo il sistema otteniamo:
f(x)=0.28221x3−1.44686x2+1.50746x1+1.26344
Esempio: Profilo di Velocità di un Fluido
Vediamo come si comporta nel fare interpolazione (non male!)...

Esempio: Profilo di Velocità di un Fluido
...E poi vediamo come va l'estrapolazione (bene anche qui!)

Elementi di Informatica e
Applicazioni Numeriche T
Polinomio di Lagrange
Metodi Espliciti e Impliciti
In questo corso facciamo spesso una distinzione tra:
- Soluzioni in forma chiusa (o metodi espliciti)
- Descrivono la soluzione con una formula
- Metodi numerici (o metodi impliciti)
- Permettono di calcolare la soluzione con un algoritmo
L'approccio presentato per ottenere il polinomio interpolante
- Permette di calcolare i coefficienti con un algoritmo...
- ...Ma non di esprimerli in forma chiusa
Si tratta quindi di un metodo numerico
Proviamo ora a vedere una soluzione in forma chiusa
Un Approccio Alternativo
Il nostro obiettivo è trovare una funzione f(x) tale che:
f(xi)=yi∀i=1..m
Proviamo ora ad utilizzare una forma diversa, in particolare:
f(x)=m∑j=1yili(x)
Dove i termini li(x) sono dei polinomi
- Conseguenza:
f(x)è di fatto ancora un polinomio - Solo che la descriviamo con una somma di funzioni...
- ...Anziché attraverso i coefficienti
Un Approccio Alternativo
Idea principale: I polinomi li(x) in
f(x)=m∑i=1yili(x)
...sono definiti in modo che, quando x=xi:
- Tutti gli
lj(xi)conj≠isi annullano - Il termine
li(xi)vale esattamente1
In questo modo, abbiamo che (come desiderato):
f(xi)=yili(xi)⏟=1+∑j≠iyjlj(xi)⏟=0=yi
Un Approccio Alternativo
Vediamo i polinomi li(x) per il nostro esempio:

Un Approccio Alternativo
Come sono fatti i polinomi li(x)?
Ogni li(x) deve annullarsi se x=xj con j≠i
- Possiamo ottenerlo inserendo in
li(x)l'espressione
∏j≠i(x−xj)
- In altre parole il prodotto:
(x−x1)…(x−xi−1)(x−xi+1)…(x−xm)
- Che si annulla per
x=xj, a meno chej=i
Un Approccio Alternativo
Come sono fatti i polinomi li(x)?
Ogni li(x) deve valere 1 per x=xi
- Possiamo ottenerlo modificando l'espressione precedente:
∏j≠i(x−xj)⟶∏j≠ix−xjxi−xj
- Ogni termine
(x−xj)/(xi−xj)vale1sex=xi - Conseguenza: l'intero prodotto vale
1
Polinomio Interpolante in Forma di Lagrange
Nel complesso, otteniamo il polinomio di Lagrange:
f(x)=m∑i=1yili(x)con: li(x)=∏j≠ix−xjxi−xj
Sarebbe meglio parlare di "polinomio interpolante in forma di Lagrange"
- È un polinomio di grado (al più)
m−1, come nel caso precedente - Di fatto, è lo stesso polinomio di prima!
- Semplicemente, adesso lo otteniamo con una formula
- In alcuni casi è un grosso vantaggio (esempi nella prossima lezione)!
Elementi di Informatica e
Applicazioni Numeriche T
Due Limitazioni dell'Interpolazione
con Polinomi
L1: Aggiunta di Punti da Interpolare
Se volessimo migliorare la qualità dell'approssimazione?
Metodo più naturale: incrementare la misurazioni
- Dividiamo il diametro in
msegmenti della stessa lunghezza - Per ogni punto
ximisuriamo la velocitàyi
Idealmente, incrementando m l'approssimazione dovrebbe convergere:
f(x)→m→∞g(x)
- Dove
g(x)è il profilo di velocità reale
In pratica, non è detto che succeda
L1: Funzione di Runge
Supponiamo di volere interpolare la funzione di Runge:
g(x)=11+25x2
Supponiamo di non conoscere g(x) direttamente
- Ne vogliamo però misurare il valore...
- ...Per punti equispaziati nell'intervallo
[−1,1] - E poi approssimarla con il polinomio interpolante
Intuitivamente:
- Incrementando
n... - ...L'approssimazione dovrebbe migliorare
L1: Funzione di Runge
Questa è la funzione di Runge nell'intervallo [−1,1]

L1: Funzione di Runge
Questo è il polinomio interpolante con n=3

L1: Funzione di Runge
Questo è il polinomio interpolante con n=5

L1: Funzione di Runge
Questo è il polinomio interpolante con n=7

L1: Funzione di Runge
Questo è il polinomio interpolante con n=9

L1: Fenomeno di Runge
- Le oscillazioni peggiorano con il numero dei campioni
- Il polinomio interpolante diverge vicino agli estremi (i.e.
−1,1)
Questo comportamento è noto come fenomeno di Runge
- È apparentemente paradossale (vedremo poi il motivo)
- È un primo (grosso) limite del polinomio approssimante
L2: Difficoltà di Estrapolazione
Consideriamo ora il secondo dei nostri esempi iniziali
- Vogliamo stimare come la velocità di una reazione chimica...
- ...Dipenda dalla temperatura a cui essa avviene
Innanzitutto dobbiamo fare degli esperimenti:
- Facciamo variare la temperature
xda300∘Ka360∘K - Usiamo intervalli di 10 gradi (
7punti in tutto) - Misuriamo la velocità di reazione ad ogni punto
L2: Difficoltà di Estrapolazione
Supponiamo di avere ottenuto i punti seguenti:
xi (°K) |
yi (num. puro) |
|---|---|
300 |
1.01 |
310 |
1.02 |
320 |
1.04 |
330 |
1.08 |
340 |
1.15 |
350 |
1.30 |
360 |
1.44 |
L2: Difficoltà di Estrapolazione
Questi sono i dati grezzi sul piano cartesiano:

L2: Difficoltà di Estrapolazione
Questo è il polinomio interpolante (in interpolazione)

L2: Difficoltà di Estrapolazione
Questo è il polinomio interpolante (in estrapolazione)

L2: Difficoltà di Estrapolazione
Il comportamento in estrapolazione è pessimo!
- Estrapolare è più difficile che interpolare in generale
- C'è un margine di incertezza maggiore
In questo caso però la situazione è particolarmente brutta, perché:
- Questo è un secondo limite del polinomio approssimante
Elementi di Informatica e
Applicazioni Numeriche T
Metodo Lineare dei Minimi Quadrati
Alcune Considerazioni
Abbiamo osservato che, aumentando il numero di punti (xi,yi):
- Il comportamento in interpolazione può peggiorare
- Il comportamento in estrapolazione può peggiorare
La radice dei due problemi è comune.
Alcune Considerazioni
Abbiamo osservato che, aumentando il numero di punti (xi,yi):
- Il comportamento in interpolazione può peggiorare
- Il comportamento in estrapolazione può peggiorare
La radice dei due problemi è comune. In particolare:
del polinomio interpolante diventa troppo alto
- I polinomi di grado elevato possono variare in modo brusco...
- ...E si prestano a causare errori dovuti alla precisione finita
Utilizzo di Polinomi di Grado Inferiore
Cosa succede se utilizziamo un polinomio di grado n<m−1?
Il nostro sistema:
Vβ=y
Dove:
Vè la matrice di Vandermonde corrispondente adxβè il vettore dei coefficienti
Diventa sovradeterminato (e probabilmente impossibile)
- Se vogliamo utilizzare un polinomio di grado inferiore...
- ...Dobbiamo cambiare la formulazione del problema
Utilizzo di Polinomi di Grado Inferiore
Vediamo le idee principali del nuovo approccio:
- Stabiliamo il grado
ndel polinomio a priori (HP:n≤m−1) - Non richiediamo che il polinomio passi per tutti i punti
- Cerchiamo invece di minimizzare una stima di errore
In particolare, introduciamo il concetto di residuo
ri=yi−f(xi)
- Dove, ancora una volta:
f(x)=n∑j=0βjxj
Residui e Stima dell'Errore
In sostanza il residuo ri è il nostro errore di stima per (xi,yi)
Idea 1: utilizziamo una somma
e=m∑i=1ri
- Una pessima idea in pratica
- Residui con segno diverso si possono cancellare
Residui e Stima dell'Errore
In sostanza il residuo ri è il nostro errore di stima per (xi,yi)
Idea 2: somma dei valori assoluti
e=m∑i=1|ri|
- Già meglio!
- Però è difficile da trattare (derivata discontinua)
Residui e Stima dell'Errore
In sostanza il residuo ri è il nostro errore di stima per (xi,yi)
Idea 3: somma dei residui al quadrato
e=m∑i=1r2i
- La derivata è continua
- Vantaggio addizionale: gli errori più grandi contano di più!
Minimizzazione ai Minimi Quadrati
Vogliamo che l'errore sia più piccolo possibile
Quindi si tratta di risolvere il problema:
min
Noto come problema di minimizzazione ai minimi quadrati
- Nel problema abbiamo evidenziato la dipendenza di
r_ida\beta - D'ora in poi, lo faremo sempre
- La soluzione
\beta^*del problema definisce la funzione approssimante - Il corrispondente errore
e^*indica la qualità dell'approssimazione
Metodo (Lineare) dei Minimi Quadrati
Nel nostro caso, per ogni punto (x_i, y_i), abbiamo:
r_i(\beta) = y_i - \sum_{j = 0} \beta_j x_i^j
- Conseguenza: i residui dipendono linearmente da
\beta - Per questa ragione, il metodo di soluzione che vedremo...
- ...Si chiama metodo lineare dei minimi quadrati
Per via della linearità, possiamo definire i residui in forma matriciale:
r = y - \underbrace{V}_{m \times (n+1)} \beta
- Dove
Vè la matrice di Vandermonde
Metodo (Lineare) dei Minimi Quadrati
Pertanto il nostro problema diventa:
\min e(\beta) = r(\beta)^T r(\beta)
r^Tè un vettore riga erun vettore colonna- Il prodotto scalare
r^T rè la somma dei residui al quadrato
Di qui otteniamo:
e(\beta) = (y - V \beta)^T (y - V \beta)
E quindi:
e(\beta) = y^T y - y^TV\beta - (V \beta)^T y - (V\beta)^T V \beta
Metodo (Lineare) dei Minimi Quadrati
A questo punto osserviamo che, nell'equazione:
e(\beta) = y^T y - y^T V \beta - (V \beta)^T y - (V\beta)^T V \beta
- Tutti i termini sono scalari e possono essere trasposti a piacimento
- Per il prodotto matriciale, vale che
(AB)^T = B^T A^T
Possiamo quindi ottenere:
e(\beta) = y^T y - (y^T V \beta)^T - (V \beta)^T y + (V\beta)^T V \beta\\
e(\beta) = y^T y - (V \beta)^T y - (V \beta)^T y + (V\beta)^T V \beta\\
e(\beta) = y^T y - 2 \beta^T V^T y + \beta^T V^T V \beta
Metodo (Lineare) dei Minimi Quadrati
A questo punto per trovare un punto estremo possiamo risolvere
\nabla e(\beta) = 0
- Poi dovremmo valutare il numero di soluzioni possibili...
- ...E verificare se corrispondano a massimi o minimi
Metodo (Lineare) dei Minimi Quadrati
A questo punto per trovare un punto estremo possiamo risolvere
\nabla e(\beta) = 0
- Poi dovremmo valutare il numero di soluzioni possibili...
- ...E verificare se corrispondano a massimi o minimi
Per poter calcolare \nabla e(\beta) in forma matriciale, è utile:
- Ottenere una formula per la "derivata" di un prodotto scalare
v^Tx - Ottenere una formula per la "derivata" di una forma quadratica
x^TAx
Nelle prossime due slides vedremo come farlo...
Digressione: Derivata di un Prodotto Scalare
Consideriamo un prodotto scalare v^T x
- Tecnicamente, si tratta di una funzione f : \mathbb{R}^n \rightarrow \mathbb{R}:
v^Tx = \sum_{i = 1}^n v_i x_i
- Il gradiente della funzione è dato da:
\nabla (v^Tx) =
\left(\begin{array}{c}
\frac{\partial (v^T x)}{x_1}\\
\vdots\\
\frac{\partial (v^T x)}{x_n}
\end{array}\right)
=
\left(\begin{array}{c}
v_1\\
\vdots\\
v_n
\end{array}\right)
= v
Digressione: Derivata di una Forma Quadratica
Consideriamo una forma quadrativca x^T A x
- Corrisponde ancora ad una funzione f : \mathbb{R}^n \rightarrow \mathbb{R}:
x^T A x = \sum_{j = 1}^n \sum_{i = 1}^n a_{ij} x_i x_j
- Derivando rispette ad
x_kotteniamo:
\frac{\partial (x^T A x)}{x_k} = \sum_{j = 1}^n a_{kj} x_j + \sum_{i = 1}^n a_{ik} x_i
Digressione: Derivata di una Forma Quadratica
Nell'espressione:
\frac{\partial (x^T A x)}{x_k} = \underbrace{\sum_{j = 1}^n a_{kj} x_j}_{\text{(A)}} + \underbrace{\sum_{i = 1}^n a_{ik} x_i}_{\text{(B)}}
I due termini (A) e (B) corrispondono a:
(A) Il prodotto scalare di una colonna di A per x
(B) Il prodotto scalare di una riga di A per x
Quindi, in forma matriciale abbiamo:
\nabla (x^T A x) = (A^T + A) x
Metodo (Lineare) dei Minimi Quadrati
A questo punto possiamo riprendere la discussione
Per trovare un polinomio approssimante, dobbiamo risolvere:
\nabla e(\beta) = 0
Dove:
e(\beta) = y^T y - 2 \beta^T V^T y + \beta^T V^T V \beta\\
e(\beta) = y^T y - 2 \underbrace{(V^T y)^T}_{vettore}\, \beta + \beta^T \underbrace{V^T V}_{matrice}\, \beta
Quindi, applicando le due regole di differenziazione matriciale:
-2 (V^T y) + (V^T V + V V^T) \beta = 0
Metodo (Lineare) dei Minimi Quadrati
La matrice V^T V è simmetrica per costruzione, infatti:
(V^T V)^T = V^T V
Quindi a partire da:
-2 (V^T y) - (V^T V + V V^T) \beta = 0
Possiamo ottenere:
-2 (V^T y) - 2 (V^T V) \beta = 0
E finalmente otteniamo un sistema lineare!
V^T V \beta = V^T y
Metodo (Lineare) dei Minimi Quadrati
- Poiché
Vè non-singolare... - ...Anche
V^Te quindiV^T Vsono non singolari
Quindi il sistema lineare:
\underbrace{V^T V}_{(n+1) \times n} \beta = \underbrace{V^T}_{(n+1) \times m} \overbrace{y}^{m \times 1}
- Ha una sola soluzione...
- ...Che corrisponde ad un estremo per
e(\beta)
Ci rimane da capire se questa corrisponda a un minimo...
Metodo (Lineare) dei Minimi Quadrati
Per capire se la soluzione del sistema corrisponda al minimo...
...Usiamo le normali regole per le funzioni multivariate:
- Calcoliamo la matrice Hessiana di
e(\beta)... - ...E ci assicuriamo che sia definita positiva
Metodo (Lineare) dei Minimi Quadrati
Per capire se la soluzione del sistema corrisponda al minimo...
...Usiamo le normali regole per le funzioni multivariate:
- Calcoliamo la matrice Hessiana di
e(\beta)... - ...E ci assicuriamo che sia definita positiva
Per ottenere H(e(\beta)) possiamo derivare nuovamente:
\nabla e(\beta) = V^T V \beta - V^T y
- Applicando la regola per
\nabla v^Txalle righe diV^T Votteniamo
H(e(\beta)) = V^T V
Metodo (Lineare) dei Minimi Quadrati
Si può dimostrare (abbastanza facilmente) che:
- Se
Vè non singolare (come nel nostro caso)... - ...Allora
V^T Vè definita positiva
Finalmente, concludiamo che risolvendo il sistema lineare:
V^T V \beta = V^T y
Otteniamo un vettore \beta di n+1 termini
- Questi sono i coefficienti di un polinomio di grado
n... - ...Che minimizza la somma dei residui al quadrato
Questo è il metodo lineare dei minimi quadrati
Matrice Pseudo-Inversa
A volte il sistema viene scritto nella forma:
\beta = (V^T V)^{-1} V^T y
- Dove
(V^T V)^{-1} V^Tè una matrice(n+1) \times m - È nota come matrice pseudo-inversa di
V
Perché parlarne? Perché se in Octave eseguite:
b = V \ y % divisione sinistra
- Se
Vè quadrata, viene risolto il sistema lineare - Se
Vè quadrata, viene risolto problema ai minimi quadrati
Di fatto eseguire questo metodo in Octave è molto facile!
Metodo dei Minimi Quadrati per l'Esempio 1
Approssimazione di grado 2 del profilo di velocità:

Metodo dei Minimi Quadrati per l'Esempio 2
Approssimazione di grado 3 della velocità di reazione:

Minimi Quadrati: Funzione di Runge
Approssimazione di grado 2 della funzione di Runge:

Minimi Quadrati: Funzione di Runge
In questo caso non funziona molto bene...

Elementi di Informatica e
Applicazioni Numeriche T
Oltre i Polinomi
Approssimazione con Funzioni Non Lineari
Nel metodo lineare dei minimi quadrati:
- Approssimiamo una funzione
g(x)... - ...Con una funzione approssimante
f(x, \beta)
Nel nostro caso f(x) era un polinomio e \beta i coefficienti
Ma potremmo usare anche qualcosa diverso dai polinomi!
Possiamo usare qualunque funzione
- Purché dipenda linearmente da
\beta... - ...dove i termini di
\betasi chiamano genericamente parametri
Approssimazione con Funzioni Non Lineari
Per la precisione, possiamo usare qualunque f(x) nella forma:
f(x, \beta) = \sum_{j = 1}^n \beta \phi_j(x)
- Dove
nè il numero dei parametri - E ogni
\phi_j(x)è una funzione arbitraria dix
In questo caso, i residui prendono la forma:
r_i(\beta) = y_i - \sum_{j = 1}^n \beta \phi_j(x_i)
- Dove
\phi_j(x_i)può essere pre-calcolato
Approssimazione con Funzioni Non Lineari
In forma matriciale abbiamo:
r(\beta) = y - \Phi \beta
Dove ogni termine della matrice \Phi_{i,j} corrisponde a \phi_j(x_i)
- La formulazione è analoga a quella dei polinomi
- Semplicemente abbiamo
\Phiinvece diV
Possiamo ottenere \beta risolvendo:
\Phi^T\Phi \beta = \Phi^T y
Esattamente come nel caso dei polinomi!
- Condizione:
\Phideve essere non singolare
Esempio: Funzione di Runge
Abbiamo avuto difficoltà ad approssimare la funzione di Runge
Proviamo ad utilizzare una funzione approssimante diversa
Per esempio:
f(x, \beta) = \beta_1 x^1 + \beta_2 \underbrace{(x^0)}_{= 1} + \beta_3 \frac{1}{1 + \left|x\right|} + \beta_4 \frac{1}{1 + x^2}
- La funzione non è un polinomio
- Però dipende linearmente dai parametri
\beta
Quindi possiamo applicare il metodo lineare dei minimi quadrati
Esempio: Funzione di Runge
Assumendo di avere x = [-1, -0.33, 0.33, 1]
- Calcoliamo la matrice
\Phi
\begin{align}
& \begin{array}{cccc}
\hspace{33mm} x_i^1 &
\hspace{20mm} x_i^0 &
\hspace{12mm} \frac{1}{1 + \left|x_i\right|} &
\hspace{12mm} \frac{1}{1 + x_i^2} &
\end{array}\\
& \Phi =
\left(\begin{array}{cccc}
-1.00000 & 1.00000 & 0.50000 & 0.50000 \\
-0.33333 & 1.00000 & 0.75000 & 0.90000 \\
0.33333 & 1.00000 & 0.75000 & 0.90000 \\
1.00000 & 1.00000 & 0.50000 & 0.50000 \\
\end{array}\right)
\end{align}
- Poi calcoliamo:
\beta = (\Phi^T \Phi) \Phi^T y
Esempio: Funzione di Runge
Otteniamo questa funzione approssimante (non un gran che):

Esempio: Funzione di Runge
Aumentando il numero di punti, però...

Esempio: Funzione di Runge
Aumentando il numero di punti, però...

Esempio: Funzione di Runge
...L'approssimazione migliora considerevolmente!
